Một con lắc đơn được treo vào trần 1 toa của đoàn tàu hỏa.

* Hướng dẫn giải

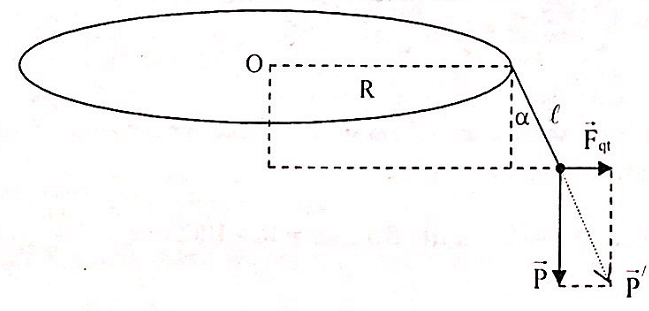
+ Vì xe chuyển động tròn đều nên xe chịu tác dụng của lực quán tính li tâm:

 \({F_{qt}} = m{\omega ^2}\left( {R + \ell \sin \alpha } \right) = m\frac{{{v^2}}}{{\left( {R + \ell \sin \alpha } \right)}}\)

+ Vì R rất lớn so với  

 \(\begin{array}{l}
\ell  \Rightarrow R >  > \ell \sin \alpha  \Rightarrow R + \ell \sin \alpha  \approx R\\
 \Rightarrow {F_{qt}} \approx m\frac{{{v^2}}}{R} \Rightarrow {g^/} = \sqrt {{g^2} + {{\left( {\frac{{{F_{qt}}}}{m}} \right)}^2}} \\
 \Rightarrow {g^/} = \sqrt {{g^2} + {{\left( {\frac{{{v^2}}}{R}} \right)}^2}}  = \sqrt {{g^2} + \left( {\frac{{{v^4}}}{{{R^2}}}} \right)} 
\end{array}\)

+ Chu kì:

\(\begin{array}{l}
T = 2\pi \sqrt {\frac{\ell }{g}}  \Rightarrow \frac{{{T^/}}}{T} = \sqrt {\frac{g}{{{g^/}}}} \\
 \Rightarrow {T^/} = T\sqrt {\frac{g}{{\sqrt {{g^2} + \left( {\frac{{{v^4}}}{{{R^2}}}} \right)} }}}  \approx 1,998\left( s \right)
\end{array}\)