Hai dao động điều hòa cùng phương theo phương trình:
Câu hỏi :
Hai dao động điều hòa cùng phương theo phương trình: \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)cm;{x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\) (cm) trên hình vẽ đường đồ thị (I) biểu diễn dao động thứ nhất, đường đồ thị (II) biểu diễn dao động tổng hợp của hai dao động. Phương trình vận tốc của dao động thứ hai là: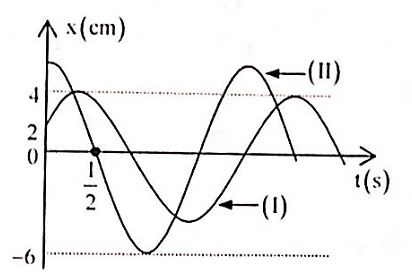
A. \({v_2} = 2\sqrt 7 \cos \left( {\pi t + 0,714} \right)\)cm/s
B. \({v_2} = 2\pi \sqrt 3 \cos \left( {\pi t + 2,285} \right)\)cm/s
C. \({v_2} = 2\pi \sqrt 7 \cos \left( {\pi t + 2,285} \right)\)cm/s
D. \({v_2} = 4\pi \sqrt 3 \cos \left( {2\pi t + 2,285} \right)\)cm/s
* Đáp án
C
* Hướng dẫn giải
+ Lúc t = 0 dao động II ở biên, đến thời điểm t = 0,5 s thì dao động II ở VTCB nên:
\(\frac{T}{4} = 0,5 \Rightarrow T = 2\left( s \right) \Rightarrow \omega = \pi \) (rad/s)
+ Lúc t = 0, dao động II đang ở biên nên phương trình dao động tổng hợp là:
x = 6cos πt (cm)
+ Lúc t = 0, vật I đang ở \(\left\{ \begin{array}{l}
{x_1} = 2\left( {cm} \right) = \frac{A}{2}\\
{v_1} > 0
\end{array} \right.\) nên phương trình dao động 1 là:
\({x_1} = 4\cos \left( {\pi t - \frac{\pi }{3}} \right)\) (cm)
+ Phương trình dao động thứ 2 là:
\(\begin{array}{l}
x = {x_1} + {x_2}\\
\Rightarrow {x_2} = x - {x_1} = 6\cos \pi t - 4\cos \left( {\pi t - \frac{\pi }{3}} \right) = 2\sqrt 7 \cos \left( {\pi t + 0,714} \right)\\
\Rightarrow {v_2} = {\left( {{x_2}} \right)^/} = 2\pi \sqrt 7 \cos \left( {\pi t + 0,714 + \frac{\pi }{2}} \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Phan Đăng Lưu
Copyright © 2021 HOCTAP247
