Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Thủ Độ
Cho hai vật nhỏ A và B có khối lượng...
Cho hai vật nhỏ A và B có khối lượng lần lượt là m1 = 900 g, m2 = 4 kg
Câu hỏi :
Cho hai vật nhỏ A và B có khối lượng lần lượt là m1 = 900 g, m2 = 4 kg đặt trên mặt phẳng nằm ngang. Hệ số ma sát trượt giữa A, B và mặt phẳng ngang đều là m = 0,1; coi hệ số ma sát nghỉ cực đại bằng hệ số ma sát trượt. Hai vật được nối với nhau bằng một lò xo nhẹ có độ cứng k = 15 N/m; B tựa vào tường thẳng đứng. Ban đầu hai vật nằm yên và lò xo không biến dạng. Vật nhỏ C có khối lượng m = 100 g bay dọc theo trục của lò xo với vận tốc v đến va chạm hoàn toàn mềm với A (sau va chạm C dính liền với A). Bỏ qua thời gian va chạm. Lấy g = 10 m/s2. Giá trị nhỏ nhất của v để B có thể dịch chuyển sang trái là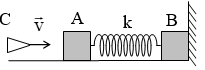
A. 1,8 m/s
B. 18 m/s
C. 9 m/s
D. 18 cm/s
* Đáp án
B
* Hướng dẫn giải
Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là xo sao cho:
Fđh = Fms =>kxo = mm2g =>150xo = 40
Như thế, vận tốc vo mà hệ (m1 + m) có khi bắt đầu chuyển động phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là xo.
Suy ra:
\[\frac{1}{2}k{x^2} = \mu ({m_1} + m)g(x + {x_o}) + \frac{1}{2}kx_o^2 \Rightarrow 75{x^2} - 10x - 8 = 0 \Rightarrow x = 0,4{\rm{ }}m.\]
Theo định luật bảo toàn năng lượng ta có:
\[\frac{1}{2}({m_1} + m)v_o^2 - \frac{1}{2}k{x^2} = \mu ({m_1} + m)gx.\]
Từ đó tính được: vo min » 1,8 m/s => vmin » 18 m/s.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Thủ Độ
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
