Điện áp \(u = {U_0}cos\left( {100\pi t} \right)\) (t tính bằng s)

* Hướng dẫn giải

Ta tính nhanh được:

\({Z_L} = 15\Omega ;{Z_C} = 10\Omega ;Z = 10\Omega \)

Góc lệch pha giữa u, ud và ue so với i qua mạch:

\[\begin{array}{*{20}{l}}
{\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{r} = \frac{1}{{\sqrt 3 }} \Rightarrow \varphi  = \frac{\pi }{6};\tan {\varphi _d} = \frac{{{Z_L}}}{r} = \sqrt 3 }\\
{ \Rightarrow \varphi  = \frac{\pi }{3}{\varphi _C} =  - \frac{\pi }{2}}
\end{array}\]

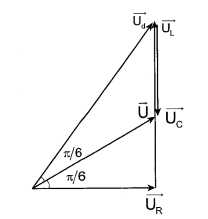
Ta có giản đồ như hình vẽ.

Theo giản đồ ta có:

\[\begin{array}{*{20}{l}}
{{U_d} = \frac{{{U_R}}}{{cos\frac{\pi }{3}}} = 2{U_R};}\\
{{U_L} = {U_R}\tan \frac{\pi }{3} = {U_R}\sqrt 3 ;}\\
{{U_L} - {U_C} = {U_R}\tan \varphi  = {U_R}\tan \frac{\pi }{6} = \frac{{{U_R}}}{{\sqrt 3 }}}
\end{array}\]

Theo bài ra ta có ud sớm pha hơn u góc π/6. Còn uc chậm pha hơn u góc 2π/3. Do đó biểu thức của ud và uc là:

\[\begin{array}{*{20}{l}}
{{u_d} = {U_d}\sqrt 2 cos\left( {100\pi t + \frac{\pi }{6}} \right) = 2{U_R}\sqrt 2 cos\left( {100\pi t + \frac{\pi }{6}} \right)V}\\
{{u_C} = {U_C}\sqrt 2 cos\left( {100\pi t - \frac{{2\pi }}{3}} \right) = \frac{{2{U_R}}}{{\sqrt 3 }}\sqrt 2 cos\left( {100\pi t - \frac{{2\pi }}{3}} \right)V}
\end{array}\]

\[\begin{array}{*{20}{l}}
{{u_d} = {U_d}\sqrt 2 cos\left( {100\pi t + \frac{\pi }{6}} \right) = 100V}\\
{{u_C} = \frac{{2{U_R}}}{{\sqrt 3 }}\sqrt 2 cos\left[ {100\pi \left( {t + \frac{1}{{15}}} \right) - \frac{{2\pi }}{3}} \right] = 100V}\\
{\left( {100\pi t + \frac{\pi }{6}} \right) = \frac{1}{{\sqrt 3 }}cos\left[ {100\pi \left( {t + \frac{1}{{15}}} \right) - \frac{{2\pi }}{3}} \right] =  =  - \frac{1}{{\sqrt 3 }}\sin \left( {100\pi t + \frac{\pi }{6}} \right)}\\
{ \Rightarrow \tan \left( {100\pi t + \frac{\pi }{6}} \right) =  - \sqrt 3  \Rightarrow cos\left( {100\pi t + \frac{\pi }{6}} \right) = \frac{1}{2}}
\end{array}\]

Mặt khác :

\[ \Rightarrow U = \frac{2}{{\sqrt 3 }}.\frac{{100}}{{\sqrt 2 }} = \frac{{200}}{{\sqrt 6 }} \Rightarrow {U_0} = U\sqrt 2  = \frac{{200\sqrt 3 }}{3} = 115V\]