Cho đoạn mạch AB. Biết R = 80 Ω, r = 20 Ω.
Câu hỏi :
Cho đoạn mạch AB. Biết R = 80 Ω, r = 20 Ω. Đặt vào hai đầu mạch một điện áp xoay chiều \(u\, = \,U\sqrt 2 \cos 100\pi t{\rm{ }}(V).\) Đồ thị biểu diễn sự phụ thuộc của điện áp tức thời giữa hai điểm A, N (uAN) và giữa hai điểm M, B (uMB) theo thời gian được biểu diễn như hình vẽ.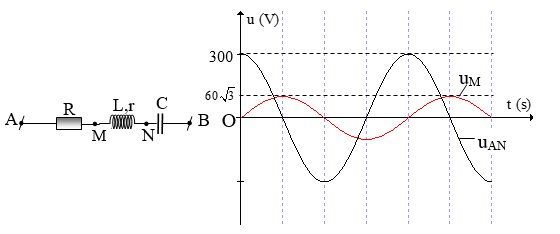
A. 0,50.
B. 0,707.
C. 0,866 V.
D. 0,945.
* Đáp án
C
* Hướng dẫn giải
Từ đồ thị ta có:
\(\begin{array}{l}
{\overrightarrow U _{AN}} \bot {\overrightarrow U _{MB}} \Leftrightarrow \tan {\varphi _{AN}}\tan {\varphi _{MB}} = - 1\\
\Leftrightarrow \frac{{{U_L}}}{{{U_R} + {U_r}}}.\frac{{{U_C} - {U_L}}}{{{U_r}}} = - 1(1)\\
R = 4r \Rightarrow {U_R} = 4{U_r}{\left( {{U_L} - {U_C}} \right)^2} = \frac{{25U_r^4}}{{U_L^2}}(2)
\end{array}\)
Mặt khác:
\(\begin{array}{l}
\left\{ \begin{array}{l}
U_{AN}^2 = {\left( {{U_R} + {U_r}} \right)^2} + U_L^2\\
U_{MB}^2 = U_r^2 + {\left( {{U_L} - {U_C}} \right)^2}
\end{array} \right.\left\{ \begin{array}{l}
{\left( {150\sqrt 2 } \right)^2} = 25U_r^2 + U_L^2\\
{\left( {30\sqrt 6 } \right)^2} = U_r^2 + \frac{{25U_r^4}}{{U_L^2}}
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
{U_r} = 15\sqrt 6 V\\
{U_L} = 75\sqrt 2 V
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
{U_R} = 60\sqrt 6 V\\
{U_C} = 120\sqrt 2 V
\end{array} \right.\\
\Rightarrow \cos \varphi = \frac{{{U_R} + {U_r}}}{{\sqrt {{{\left( {{U_R} + {U_r}} \right)}^2} + {{\left( {{U_L} - {U_C}} \right)}^2}} }} = \frac{{5\sqrt 7 }}{{14}} = 0,945.
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Thủ Độ
Copyright © 2021 HOCTAP247
