Giao thoa sóng ở mặt nước với hai nguồn kết hợp đặt tại A và B

* Hướng dẫn giải

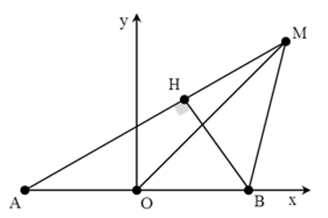
Các cực đại giao thoa tạo thành các dãy hypebol

Trong hệ trục tọa độ đã chọn d có phương trình y=x

Gọi N là điểm cực đại trên d gần O nhất, khi đó N thuộc cực đại ứng với k=0

Ta có: 

\(\left\{ \begin{array}{l}
c = \frac{{AB}}{2} = 10\\
a = \frac{{0,5\lambda }}{2} = 0,75
\end{array} \right. \Rightarrow y = \sqrt {\left( {{c^2} - {a^2}} \right)\left( {\frac{{{x^2}}}{{{a^2}}} - 1} \right)}  = \sqrt {99,4375\left( {\frac{{{x^2}}}{{0,5625}} - 1} \right)} \)

Phương trình gia điểm giữa d và y: 

\(y = x \Leftrightarrow 99,4375\left( {\frac{{{x^2}}}{{0,5625}} - 1} \right) = {x^2} \Rightarrow {x_N} = 0,75{\rm{ }}cm.\)

+Gọi M là điểm cực đại trên d xa N nhất, khi M tiến về vô cùng thì \(AM - BM \approx AB\cos 45^\circ  = 10\sqrt 2 .\) 

Xét tỉ số (AM-BM)/λ=4,7 => M xa N nhất thuộc cực đại ứng với n=4=> a=6,75

+ Khoảng cách giữa M và N: 

\(\begin{array}{l}
y = \sqrt {\left( {{c^2} - {a^2}} \right)\left( {\frac{{{x^2}}}{{{a^2}}} - 1} \right)}  = \sqrt {54,4375\left( {\frac{{{x^2}}}{{45,5625}} - 1} \right)} \\
y = x\\
 \Leftrightarrow y = 54,4375\left( {\frac{{{x^2}}}{{45,5625}} - 1} \right) = {x^2} \Rightarrow {x_M} = 16,7\\
MN = \frac{{{x_M} - {x_N}}}{{\cos 45^\circ }} \approx 22,6{\rm{ }}cm.
\end{array}\)