Trong hiện tượng giao thoa sóng nước, hai nguồn A, B cách nhau 10 cm

* Hướng dẫn giải

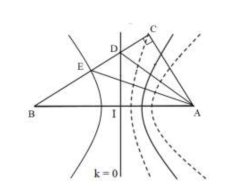
Ta có: \(AC=\sqrt{A{{B}^{2}}-B{{C}^{2}}}=\sqrt{{{10}^{2}}-{{8}^{2}}}=6\left( cm \right)\)

Tại điểm C có: \(BC-AC=2\left( cm \right)=\frac{\lambda }{2}\to \) điểm C thuộc đường cực tiểu bậc 1

=> Để trên CB có 2 điểm cực đại gần nhau nhất, D và E thuộc đường cực đại bậc 0 và bậc 1 (như hình vẽ)

D nằm trên cực đại bậc 0, ta có:

\(DA=DB=x\Rightarrow x+\sqrt{{{x}^{2}}-{{6}^{2}}}=8\Rightarrow x=6,25\left( cm \right)\)

Điểm E nằm trên cực đại bậc 1, ta có: \(EA-EB=\lambda \Rightarrow EA=EB+\lambda \)

Đặt \(EB=y\Rightarrow EA=y+4\)

\(\Rightarrow y+\sqrt{{{\left( y+4 \right)}^{2}}-{{6}^{2}}}\Rightarrow y=3,5\left( cm \right)\)

\(\Rightarrow DE=x-y=6,25-3,5=2,75\left( cm \right)\)

Giá trị tìm được gần nhất với giá trị 2,8 cm