Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lục Ngạn
Đặt vào hai đầu đoạn mạch \(RLC\) nối tiếp một...
Đặt vào hai đầu đoạn mạch \(RLC\) nối tiếp một điện áp xoay chiều
Câu hỏi :
Đặt vào hai đầu đoạn mạch \(RLC\) nối tiếp một điện áp xoay chiều \(u=200\cos \left( \omega t \right)\)V. Biết \(R=10\)Ω và \(L\), \(C\) là không đổi. Đồ thị biểu diễn sự phụ thuộc của \({{Z}_{L}}\) và \({{Z}_{C}}\) vào \(\omega \) được cho như hình vẽ. Tổng tở của mạch khi \(\omega ={{\omega }_{1}}\) là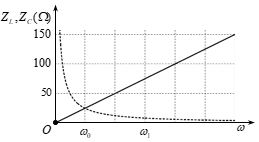
A. 10 Ω.
B. 20 Ω.
C. \(\frac{25}{3}\) Ω.
D. 67,4 Ω.
* Đáp án
D
* Hướng dẫn giải
Dễ thấy, đường nét liền biểu diễn \({{Z}_{L}}\), nét đứt biểu diễn \({{Z}_{C}}\).
+ Từ đồ thị ta có:
tại \(\omega =2{{\omega }_{0}}\) thì \({{Z}_{L}}=50\)Ω → \({{Z}_{L0}}=25\)Ω.
tại \(\omega ={{\omega }_{0}}\) → cộng hưởng → \({{Z}_{L0}}={{Z}_{C0}}=25\)Ω.
tại \(\omega ={{\omega }_{1}}=3{{\omega }_{0}}\)→
\(\left\{ \begin{array}{l}
{Z_1} = 3{Z_{L0}} = 75\\
{Z_{C1}} = \frac{{{Z_{C0}}}}{3} = \frac{{25}}{3}
\end{array} \right.\)
→ \(Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L1}}-{{Z}_{C1}} \right)}^{2}}}=\sqrt{{{10}^{2}}+{{\left( 75-\frac{25}{3} \right)}^{2}}}=67,4\)Ω.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lục Ngạn
Số câu hỏi: 39
Copyright © 2021 HOCTAP247
