Biết năng lượng ứng với các trạng thái dừng của nguyên tử Hidro được tính theo biểu thức

* Hướng dẫn giải

Do đám khí chỉ phát ra một bức xạ đơn sắc nên bức xạ này tương ứng sự dịch chuyền mức năng lượng \){{E}_{2}}-{{E}_{1}}\), có nghĩa là mức năng lượng kích thích cao nhất của đám khí khi đó là E₂, ứng với quỹ đạo L, ta có: \(h{{f}_{1}}={{E}_{2}}-{{E}_{1}}\) (1)

Khi chiếu bức xạ có tần số \({{f}_{2}}=1,25{{f}_{1}}\) thì ta có \(h{{f}_{2}}={{E}_{n}}-{{E}_{1}}\)  (2)

Từ (1) và (2) ta có \(\frac{h{{f}_{2}}}{h{{f}_{1}}}=\frac{{{E}_{n}}-{{E}_{1}}}{{{E}_{2}}-{{E}_{1}}}\Rightarrow \frac{-\frac{{{E}_{0}}}{{{n}^{2}}}-\left( -\frac{{{E}_{0}}}{{{1}^{2}}} \right)}{-\frac{{{E}_{0}}}{{{2}^{2}}}-\left( -\frac{{{E}_{0}}}{{{1}^{2}}} \right)}=1,25\)

\(\Rightarrow \frac{-\frac{1}{{{n}^{2}}}+1}{-\frac{1}{{{2}^{2}}}+1}=1,25\Rightarrow n=4\)

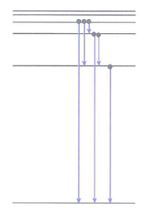
Như vậy mức năng lượng kích thích cao nhất trong trường hợp này là mức E₄.

Số loại bức xạ do khối khí phát ra là \(N=\frac{4\left( 4-1 \right)}{2}=6\) loại.