Hai dòng điện không đổi có cường độ \({{I}_{1}}=6A\) và \({{I}_{2}}=9A\)
Câu hỏi :
Hai dòng điện không đổi có cường độ \({{I}_{1}}=6A\) và \({{I}_{2}}=9A\) chạy ngược chiều trong hai dây dẫn thẳng, rất dài, song song với nhau và cách nhau 10 cm trong chân không. Cảm ứng từ do hệ hai dòng điện gây ra tại điểm M cách dây dẫn mang dòng điện I1 một đoạn 6 cm và cách dây dẫn mang dòng điện I2 một đoạn 8 cm có độ lớn bằng
A. \({{3.10}^{-5}}T\)
B. \({{0,25.10}^{-5}}T\)
C. \({{4,25.10}^{-5}}T\)
D. \({{3,3.10}^{-5}}T\)
* Đáp án
A
* Hướng dẫn giải
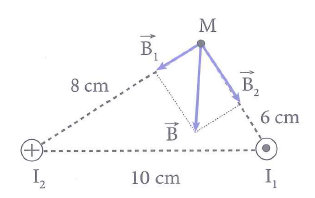
Cảm ứng từ do từng dòng điện I1 và I2 gây ra tại điểm M là
\({{B}_{1}}={{2.10}^{-7}}.\frac{{{i}_{1}}}{{{r}_{1}}}={{2.10}^{-7}}.\frac{6}{0,06}={{2.10}^{-5}}T\)
\({{B}_{2}}={{2.10}^{-7}}.\frac{{{i}_{2}}}{{{r}_{2}}}={{2.10}^{-7}}.\frac{9}{0,08}={{2,25.10}^{-5}}T\)
Do mối liên hệ giữa cách khoảng cách là \({{10}^{2}}={{6}^{2}}+{{8}^{2}}\) thỏa mãn định lý Pitago nên các véc tơ cảm ứng từ tại M vuông góc với nhau, \({{\overrightarrow{B}}_{1}}\bot {{\overrightarrow{B}}_{2}}\).
Suy ra cảm ứng từ tại M là \(B=\sqrt{B_{1}^{2}+B_{2}^{2}}=\sqrt{{{\left( {{2.10}^{-5}} \right)}^{2}}+{{\left( {{2,25.10}^{-5}} \right)}^{2}}}={{3.10}^{-5}}T\) .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Phương Sơn
Copyright © 2021 HOCTAP247
