Đặt điện áp xoay chiều \(u={{U}_{0}}\cos \omega t\) (\omega \) thay đổi
Câu hỏi :
Đặt điện áp xoay chiều \(u={{U}_{0}}\cos \omega t\) (\(\omega \) thay đổi được) vào hai đầu đoạn mạch AB như Hình H1, trong đó R là biến trở, tụ điện có điện dung \(C=125\mu F\), cuộn dây có điện trở r và độ tự cảm \(L=0,14\,H\). Ứng với mỗi giá trị của R, điều chỉnh \(\omega ={{\omega }_{R}}\) sao cho điện áp giữa hai đầu đoạn mạch AN và điện áp giữa hai đầu đoạn mạch MB vuông pha với nhau. Hình H2 biểu diễn sự phụ thuộc của \(\frac{1}{\omega _{R}^{2}}\) theo R. Giá trị của r là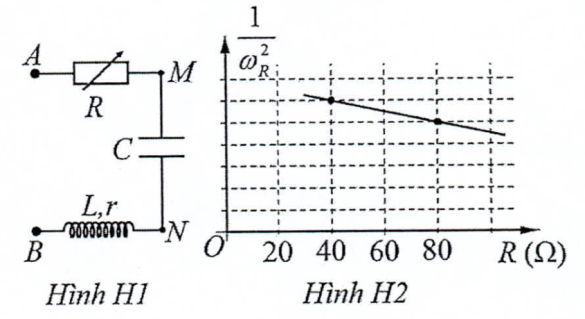
A. \(5,6\Omega \)
B. \(4\Omega \)
C. \(28\Omega \)
D. \(14\Omega \)
* Đáp án
B
* Hướng dẫn giải
Ta có: \(\overrightarrow{{{U}_{AN}}}\bot \overrightarrow{{{U}_{MB}}}\)
\(\Rightarrow \frac{{{Z}_{C}}}{R}.\frac{{{Z}_{L}}-{{Z}_{C}}}{r}=1\Leftrightarrow R.r={{Z}_{C}}.{{Z}_{L}}-Z_{C}^{2}\Rightarrow R.r=\frac{1}{C\omega }.L\omega -\frac{1}{{{C}^{2}}.{{\omega }^{2}}}\)
Đặt:
\(\left\{ \begin{array}{l}
R = y\\
\frac{1}{{{\omega ^2}}} = x
\end{array} \right. \Rightarrow y = b - a \Rightarrow \left\{ \begin{array}{l}
b = \frac{L}{{C.r}}\\
a = \frac{1}{{{C^2}.r}}
\end{array} \right.\)
Từ đồ thị (chuẩn hóa \(\frac{1}{{{\omega }^{2}}}\)) suy ra:
\(\begin{array}{l}
y = 40 \Rightarrow x = 6 \Rightarrow 40 = b - 6.a\\
y = 80 \Rightarrow x = 5 \Rightarrow 80 = b - 5.a\\
\Rightarrow \left\{ \begin{array}{l}
b = 280\\
a = 40
\end{array} \right. \Rightarrow \frac{L}{{C.r}} = 280 \Rightarrow r = 4\Omega
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Tân Yên
Copyright © 2021 HOCTAP247
