Hai chất điểm dao động điều hòa cùng tần số có li độ phụ thuộc thời gian

* Hướng dẫn giải

Ta xét trong khoảng thời gian từ lúc \(t=0s\) đến lúc \(t=2s\), dựa vào đồ thị li độ có thể thấy:

- Chất điểm (1) đi từ vị trí ban đầu về lại vị trí cũ nhưng đổi chiều chuyển động

- Chất điểm (2) đi từ vị trí ban đầu đến biên dương lần đầu tiên.

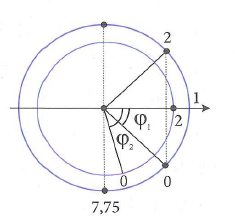
Biểu diễn các quá trình trên lên hai đường tròn đồng tâm như hình vẽ. Do cùng khoảng thời gian nên góc quét của hai chuyển động tròn đều là bằng nhau, ta suy ra mối quan hệ của hai góc \({{\varphi }_{2}}=2{{\varphi }_{1}}\) (1).

Đến thời điểm \(t=7,75s\) ta thấy chất điểm (1) qua VTCB theo chiều dương, suy ra góc quét trên đường tròn \({{\Delta }_{1}}=\omega .7,75={{\varphi }_{1}}+\frac{3\pi }{2}\) (2)

Đến thời điểm \(t=2s\) thì chất điểm (2) qua vị trí biên dương, góc quét khi đó là \({{\Delta }_{2}}=\omega .2={{\varphi }_{2}}\) (3)

Từ (2) và (3) ta có \(\frac{31}{8}=\frac{{{\varphi }_{1}}+\frac{3\pi }{2}}{{{\varphi }_{2}}}\) (4).

Tù (1) và (4) ta tìm được \({{\varphi }_{1}}=\frac{2\pi }{9};\,{{\varphi }_{2}}=\frac{4\pi }{9}\) và chu kì \(T=9s\), suy ra \(\omega =\frac{2\pi }{9}rad/s\)

Ta có giá trị cực đại \({{v}_{1max}}={{A}_{1}}\omega =4.\frac{2\pi }{9}=\frac{8\pi }{9}cm/s\); \({{v}_{2max}}={{A}_{2}}\omega =2\sqrt{3}.\frac{2\pi }{9}=\frac{4\sqrt{3}\pi }{9}cm/s\) và v₁ sớm pha hơn v₂ là \(\frac{2\pi }{9}\).

Biểu diễn trên đường tròn đa trục, chất điểm (1) đến điểm M có \({{v}_{1}}=\frac{4\pi }{9}m/s=\frac{{{v}_{1max}}}{2}\) thì chất điểm (2) đến N.

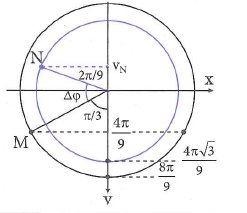
Từ đó suy ra khi

\({{v}_{2}}={{v}_{2max}}.cos\left( \pi -\frac{2\pi }{9}-\frac{\pi }{3} \right)=\frac{4\sqrt{3}\pi }{9}.cos\left( \frac{4\pi }{9} \right)\approx 0,42cm/s\)