Một vật có khối lượng 400 g dao động điều hòa.

* Hướng dẫn giải

Từ đồ thị ta thấy khoảng thời gian giữa 2 ô là: \(\frac{2}{3}-\frac{1}{3}=\frac{1}{3}\left( s \right)\)

Chu kì biến thiên của thế năng là 3 ô \(\Rightarrow T'=\frac{3}{2}.\frac{1}{3}=0,5\left( s \right)\)

Thế năng biến thiên với chu kì: \(T'=\frac{T}{2}\Rightarrow T=2T'=2.0,5=1\left( s \right)\)

Tại thời điểm \(t=0,\) thế năng của vật đang giảm \(\to \) li độ giảm.

Ta có:

\({{\text{W}}_{t}}=15\left( mJ \right)=\frac{3}{4}{{\text{W}}_{t\max }}=\frac{3}{4}\text{W}\Rightarrow \text{W}=\frac{4}{3}{{\text{W}}_{t}}\Rightarrow x=\pm \frac{1}{\sqrt{\frac{4}{3}}}A=\pm \frac{A\sqrt{3}}{2}\)

Tại thời điểm \(t=0,\) vật chuyển động theo chiều dương, ta có vòng tròn lượng giác:

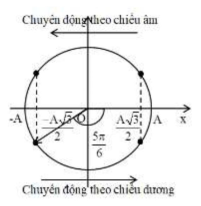
Từ vòng tròn lượng giác, ta thấy pha ban đầu của dao động là: \(\varphi =-\frac{5\pi }{6}\left( rad \right)\)

Thế năng cực đại của vật là:

\({{\text{W}}_{t\max }}=\text{W}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow {{20.10}^{-3}}=\frac{1}{2}.0,4.{{\left( 2\pi  \right)}^{2}}.{{A}^{2}}\)

\(\Rightarrow A=0,05\left( m \right)=5\left( cm \right)\)

Phương trình dao động của vật là: \(x=5\cos \left( 2\pi t-\frac{5\pi }{6} \right)\left( cm \right)\)