Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m

* Hướng dẫn giải

Tần số góc của con lắc là: \(\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{0,1}}=10\sqrt{10}=10\pi \left( rad/s \right)\)

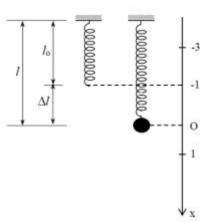
Ở VTCB, lò xo giãn một đoạn là:

\(\Delta {{l}_{0}}=\frac{mg}{k}=\frac{0,1.10}{100}=0,01\left( m \right)=1\left( cm \right)\)

Nâng vật lên để lò xo nén 3 cm, li độ của con lắc khi đó là:

\(x=-\left( 3+1 \right)=-4\left( cm \right)\)

Ta có công thức độc lập với thời gian:

\({{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\Rightarrow {{\left( -4 \right)}^{2}}+\frac{{{\left( 30\pi  \right)}^{2}}}{{{\left( 10\pi  \right)}^{2}}}={{A}^{2}}\Rightarrow A=5\left( cm \right)\)

Độ lớn của lực đàn hồi là:

\({{F}_{dh}}=k\Delta l\Rightarrow \Delta l=\frac{{{F}_{dh}}}{k}\Rightarrow \Delta l<\frac{2}{100}=0,02\left( m \right)=2\left( cm \right)\)

\(\Rightarrow -3<x<1\left( cm \right)\)

Ta có vòng tròn lượng giác:

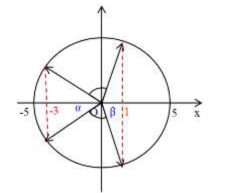
Từ vòng tròn lượng giác, ta có:

\(\left\{ \begin{align} & cos\alpha =\frac{3}{5}\Rightarrow \alpha \approx {{53}^{0}} \\ & cos\beta =\frac{1}{5}\Rightarrow \beta \approx {{78}^{0}} \\ \end{align} \right.\)

Vậy trong khoảng thời gian lực đàn hồi có độ lớn nhỏ hơn 2 N, vecto quay được góc:

\(\Delta \varphi =2.\left( 180-53-78 \right)={{98}^{0}}\approx 1,71\left( rad \right)\)

\(\Rightarrow \Delta t=\frac{\Delta \varphi }{\omega }=\frac{1,71}{10\pi }=0,054\left( s \right)\)

Vậy giá trị thời gian gần nhất là 0,05 s