Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k
Câu hỏi :
Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k = 10N/m, khối lượng của vật nặng là m = 100g, vật đang đứng yên ở vị trí cân bằng. Kéo vật dọc theo trục lò xo, ra khỏi vị trí cân bằng một đoạn \(3\sqrt{2}\)cm rồi thả nhẹ, sau đó vật dao động điều hòa dọc theo trục Ox trùng với trục lò xo, gốc O tại vị trí cân bằng của vật. Chọn gốc thời gian t = 0 là lúc vật qua vị trí x = -3cm theo chiều dương. Phương trình dao động của vật là
A. \(x=3\sqrt{2}.\cos \left( 10t+\frac{3\pi }{4} \right)\text{cm}\)
B. \(x=3.\cos \left( 10t-\frac{3\pi }{4} \right)cm\)
C. \(x=3\sqrt{2}.\cos \left( 10t-\frac{3\pi }{4} \right)\text{cm}\)
D. \(x=3\sqrt{2}.\cos \left( 10t-\frac{\pi }{4} \right)\text{cm}\)
* Đáp án
C
* Hướng dẫn giải
Tần số góc: \(\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0,1}}=10\text{rad}/\text{s}\)
Kéo vật ra khỏi VTCB đoạn \(3\sqrt{2}\text{cm}\)rồi thả nhẹ \(\Rightarrow A=3\sqrt{2}cm\)
Tại t = 0 vật qua vị trí x = -3cm theo chiều dương. Biểu diễn trên VLTG ta có:
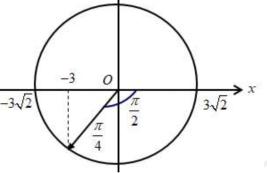
Từ VTLG \(\Rightarrow \) Pha ban đầu: \(\varphi =-\left( \frac{\pi }{2}+\frac{\pi }{4} \right)=-\frac{3\pi }{4}\)
\(\Rightarrow x=3\sqrt{2}.\cos \left( 10t-\frac{3\pi }{4} \right)\text{cm}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Nguyễn Trãi - Hải Dương
Copyright © 2021 HOCTAP247
