Một sợi dây nhẹ không dãn có chiều dài 1,5m được cắt thành hai con lắc đơn
Câu hỏi :
Một sợi dây nhẹ không dãn có chiều dài 1,5m được cắt thành hai con lắc đơn có chiều dài khác nhau. Kích thích cho hai con lắc dao động điều hòa tại nơi có gia tốc trọng trường g = 9,8m/s2. Hình vẽ bên là đồ thị phụ thuộc thời gian của các li độ góc của các con lắc. Tốc độ dao động cực đại của vật nặng con lắc (2) gần giá trị nào nhất sau đây? 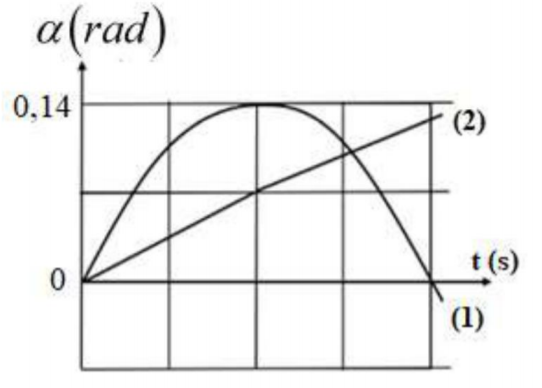
A. 0,17 m/s
B. 1,08 m/s
C. 0,51 m/s
D. 180,24 m/s
* Đáp án
A
* Hướng dẫn giải
Từ đồ thị, ta có:
+ Biên độ góc của con lắc thứ nhất: \({{\alpha }_{01}}=0,14(\text{rad})\)
T1 tương ứng 8 ô
+ Ban đầu t = 0: Cả 2 con lắc đều ở VTCB theo chiều dương.
Đến thời điểm con lắc 1 lên VT biên độ góc thì con lắc 2 có li độ \({{\alpha }_{2}}=\frac{{{\alpha }_{01}}}{2}\)
Đến thời điểm con lắc 1 và 2 cùng li độ nhưng ngược chiều nhau
Ta suy ra: \({{\alpha }_{01}}={{\alpha }_{02}}\)
+ Lại có:
\({{l}_{1}}+{{l}_{2}}=1,5~\text{ }va\text{ }~\frac{{{\omega }_{1}}}{{{\omega }_{2}}}=3=\sqrt{\frac{{{l}_{2}}}{{{l}_{1}}}}\text{ }\Rightarrow \text{ }\frac{{{l}_{2}}}{{{l}_{1}}}=\text{9 }\Rightarrow \left\{ \begin{array}{*{35}{l}} {{l}_{1}}=1,35m \\ {{l}_{2}}=0,15m \\ \end{array} \right.\)
Tốc độ dao động cực đại của con lắc (2): \({{v}_{{{2}_{\max }}}}=\sqrt{2g{{l}_{2}}\left( 1-\cos {{\alpha }_{02}} \right)}=0,169m/s\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Hạ Long - Quảng Ninh
Copyright © 2021 HOCTAP247
