Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Xét 3 phần tử A, B, C

* Hướng dẫn giải

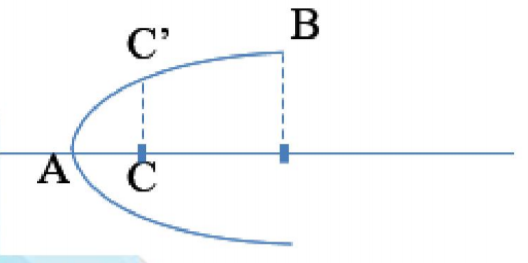
Ta có: \(AB=\frac{\lambda }{4}=21\text{cm}\Rightarrow \lambda =84\text{cm}\Rightarrow AC=\frac{AB}{3}=\frac{\lambda }{12}=7\text{cm}\)

Biên độ của B: \({{a}_{B}}=2\text{a}\) (điểm bụng) 

Biên độ của C: \({{a}_{C}}=2a\sin \frac{2\pi d}{\lambda }=2a\sin \frac{2\pi \frac{\lambda }{12}}{\lambda }=a\)

Khi dây bị biến dạng nhiều nhất khi đó AC' = 9cm

Lại có: \(A{{C}^{\prime 2}}=A{{C}^{2}}+{{a}^{2}}\Rightarrow a=4\sqrt{2}cm\)

+ Tốc độ dao động cực đại của phần tử B: \({{v}_{B}}=2\text{a}\omega \)

+ Tốc độ truyền sóng trên dây: \(v=\lambda f=\lambda \frac{\omega }{2\pi }\)

\(\Rightarrow \) Tỉ số giữa tốc độ dao động cực đại của phần tử B và tốc độ truyền sóng: \(\frac{2a\omega }{\lambda \frac{\omega }{2\pi }}=\frac{4a}{\lambda }=\frac{4\pi .4\sqrt{2}}{84}=0,846\)