Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Hạ Long - Quảng Ninh
Đặt một điện áp xoay chiều ổn định \(u=U\sqrt{2}\cos (\omega...
Đặt một điện áp xoay chiều ổn định \(u=U\sqrt{2}\cos (\omega t)\) V
Câu hỏi :
Đặt một điện áp xoay chiều ổn định \(u=U\sqrt{2}\cos (\omega t)\) V vào hai đầu một đoạn mạch ghép nối tiếp gồm điện trở R, một cuộn cảm thuần có độ tự cảm L và một tụ điện có điện dung C thay đổi được. Gọi i là cường độ dòng điện tức thời qua mạch, \(\varphi \) là độ lệch pha giữa u và i. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của tan\(\varphi \) theo ZC. Thay đổi C để điện áp hai đầu đoạn mạch vuông pha với điện áp hai đầu đoạn mạch RL, giá trị của dung kháng khi đó là 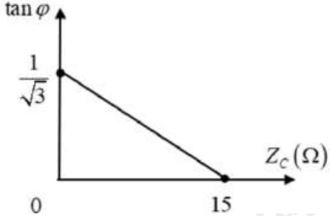
A. \(15\sqrt{3}\Omega \)
B. 30Ω
C. 15Ω
D. 60Ω
* Đáp án
D
* Hướng dẫn giải
Từ đồ thị, ta có:
+ Khi \(\tan \varphi =0\) hay \(\varphi =0\) thì \({{Z}_{L}}={{Z}_{C}}=15\Omega \)
+ Khi \(\tan {{\varphi }_{1}}=\frac{1}{\sqrt{3}}\) thì \({{Z}_{C}}=0\)
Khi đó, \(\tan {{\varphi }_{1}}=\frac{15-0}{R}\Rightarrow R=\frac{15}{\frac{1}{\sqrt{3}}}=15\sqrt{3}\Omega \)
Khi \({{u}_{RL}}\bot u\) (C thay đổi để \({{U}_{C\max }}\)) khi đó:
\({{Z}_{C}}=\frac{{{R}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}=\frac{{{(15\sqrt{3})}^{2}}+{{15}^{2}}}{15}=60\Omega \)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Hạ Long - Quảng Ninh
Số câu hỏi: 39
Copyright © 2021 HOCTAP247
