Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà
Câu hỏi :
Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà theo thời gian được mô tả bằng đồ thị ở hình bên. Biểu thức cường độ dòng điện tức thời của đoạn mạch đó là: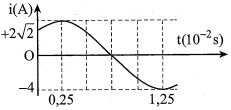
A. \(i=4\cos \left( 100\pi t+\frac{\pi }{4} \right)A\)
B. \(i=4\cos \left( 120\pi t-\frac{\pi }{4} \right)A\)
C. \(i=4\cos \left( 100\pi t-\frac{\pi }{4} \right)A\)
D. \(i=4\cos \left( 120\pi t+\frac{\pi }{4} \right)A\)
* Đáp án
C
* Hướng dẫn giải
Từ đồ thị, ta có điểm thấp nhất ứng với: \(i=-4\text{A}=-{{I}_{0}}\Rightarrow {{I}_{0}}=4\text{A}\).
Từ thời điểm \({{t}_{1}}=0,{{25.10}^{-2}}s\) đến thời điểm \({{t}_{2}}=1,{{25.10}^{-2}}s\) dòng điện giảm từ giá trị \({{I}_{0}}\) đến \(-{{I}_{0}}\) nên thời gian tương ứng là: \(\Delta t={{t}_{2}}-{{t}_{1}}=\frac{T}{2}\Rightarrow T=0,02\text{s}\Rightarrow \omega =100\pi \text{ rad/s}\).
Tại \(t=0\) có \(i=2\sqrt{2}A=\frac{{{I}_{0}}}{\sqrt{2}}\Rightarrow {{\varphi }_{0}}=\pm \frac{\pi }{4}\) và đang tăng \(\Rightarrow {{\varphi }_{0}}=-\frac{\pi }{4}\).
Vậy phương trình của i: \(i=4\cos \left( 100\pi t-\frac{\pi }{4} \right)A\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Giá Rai
Copyright © 2021 HOCTAP247
