Một con lắc lò xo treo thẳng đứng có độ lớn lực đàn hồi của lò xo
Câu hỏi :
Một con lắc lò xo treo thẳng đứng có độ lớn lực đàn hồi của lò xo biến đổi theo thời gian như hình vẽ bên. Lấy g = 10m/s2, p2 = 10. Cơ năng dao động của vật bằng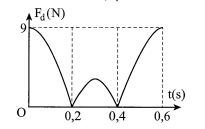
A. 0,54 J.
B. 0,18 J.
C. 0,38 J.
D. 0,96 J.
* Đáp án
A
* Hướng dẫn giải
Lực đàn hồi của lò xo đạt cực đại ở biên dưới nên khoảng thời gian liên tiếp giữa hai lần lực đàn hồi cực đại là chu kì T. Từ đồ thị ta thấy T = 0,6 s.
Lực đàn hồi bằng 0 khi đi qua vị trí lò xo không biến dạng.
Từ đồ thị ta thấy khoảng thời gian giữa 2 lần lực đàn hồi có độ lớn bằng 0 là:
\(\Delta t=0,4-0,2=0,2\left( s \right)=\frac{T}{3}\)
Góc quét tương ứng là: \(\Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{3}=\frac{2\pi }{3}\)
Ta có vòng tròn lượng giác:

Từ vòng tròn lượng giác, ta có: \(\Delta {{\ell }_{0}}=A\cos \frac{\pi }{3}=\frac{A}{2}\)
Chu kì của con lắc là: \(T=2\pi \sqrt{\frac{m}{k}}=2\sqrt{\frac{\Delta {{\ell }_{0}}}{g}}=0,6\left( s \right)\)
\(\Rightarrow 2\pi \sqrt{\frac{A}{2g}}=0,6\Rightarrow 2\sqrt{10}.\sqrt{\frac{A}{2.10}}=0,6\Rightarrow A=0,18\left( m \right)\)
Độ lớn lực đàn hồi cực đại là: \({{F}_{h\max }}=k\left( A+\Delta {{\ell }_{0}} \right)=k.\frac{3A}{2}\Rightarrow k.\frac{3.0,18}{2}=9\Rightarrow k=\frac{100}{3}\left( N\text{/}m \right)\)
Cơ năng của vật là: \(\text{W}=\frac{1}{2}k{{A}^{2}}=\frac{1}{2}.\frac{100}{3}.0,{{18}^{2}}=0,54\left( J \right)\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Hiệp Thành
Copyright © 2021 HOCTAP247
