Hai điểm sáng cùng dao động điều hoà trên trục Ox nằm ngang

* Hướng dẫn giải

Phương trình vận tốc của hai chất điểm:

\(\left\{ \begin{align} & {{v}_{1}}=20\pi \cos \left( 5\pi t+\frac{\pi }{2} \right) \\ & {{v}_{1}}=20\pi \sqrt{3}\cos \left( 5\pi t+\frac{\pi }{6}+\frac{\pi }{2} \right)=20\pi \sqrt{3}\cos \left( 5\pi t+\frac{2\pi }{3} \right) \\ \end{align} \right.\)

Ta có: \(d={{x}_{1}}-{{x}_{2}}=A\cos \left( \omega t+\varphi  \right)\)

Với: \(\tan \varphi =\frac{4\sin 0-4\sqrt{3}\sin \frac{\pi }{6}}{4\cos 0-4\sqrt{3}\cos \frac{\pi }{6}}=\sqrt{3}\Rightarrow \varphi =\frac{\pi }{3}\Rightarrow d=A\cos \left( 5\pi t+\frac{\pi }{3} \right)\Rightarrow {{d}_{\max }}=A\Leftrightarrow d=\pm A\)

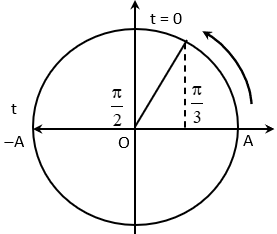
Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác:

Góc quét được: \(\alpha =\frac{\pi }{6}+\frac{\pi }{2}=\frac{2\pi }{3}\Rightarrow t=\frac{\alpha }{\omega }=\frac{\frac{2\pi }{3}}{5\pi }=\frac{2}{25}s\).

Tại \(t=\frac{2}{15}s\) tỉ số vận tốc của chất điểm 1 so với chất điểm 2:

\(\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{20\pi \cos \left( 5\pi .\frac{2}{15}+\frac{\pi }{2} \right)}{20\pi \sqrt{3}\cos \left( 5\pi .\frac{2}{15}+\frac{2\pi }{3} \right)}=\frac{-\frac{\sqrt{3}}{2}}{-\frac{\sqrt{3}}{2}}=1\).