Đặt điện áp \(u=U\sqrt{2}\cos 2\pi ft\) (U không đổi, f thay đổi được)
Câu hỏi :
Đặt điện áp \(u=U\sqrt{2}\cos 2\pi ft\) (U không đổi, f thay đổi được) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở R, cuộn cảm thuần L và tụ điện C. Khi f = 25 Hz thì u sớm pha hơn \({{u}_{C}}\) là 60°. Hình vẽ bên là đồ thị phụ thuộc f của công suất mạch tiêu thụ. Giá trị P3 gần giá trị nào nhất sau đây?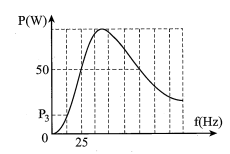
A. 10 W.
B. 9,2 W.
C. 6,5 W.
D. 18 W.
* Đáp án
D
* Hướng dẫn giải
Từ đồ thị ta thấy 2 ô ứng với tần số 25Hz suy ra 1 ô ứng với tần số 12,5 Hz.
Với \({{f}_{1}}=25\text{ }Hz\) và \({{f}_{2}}=75\text{ }Hz\), công suất tiêu thụ trên mạch có cùng giá trị:
\({{P}_{1}}={{P}_{2}}\Rightarrow \frac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}^{2}}}=\frac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}^{2}}}\)
\(\Rightarrow {{\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}^{2}}={{\left( {{Z}_{{{L}_{2}}}}-{{Z}_{{{C}_{2}}}} \right)}^{2}}\)
Lại có: \({{f}_{2}}=3{{f}_{1}}\Rightarrow \left\{ \begin{align} & {{Z}_{{{L}_{2}}}}=3{{Z}_{{{L}_{1}}}} \\ & {{Z}_{{{C}_{2}}}}=\frac{1}{3}{{Z}_{{{C}_{1}}}} \\ \end{align} \right.\)
\(\Rightarrow {{\left( {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}} \right)}^{2}}={{\left( 3{{Z}_{{{L}_{1}}}}-\frac{1}{3}{{Z}_{{{C}_{1}}}} \right)}^{2}}\)
\(\Rightarrow \left( \begin{align} & {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}}=3{{Z}_{{{L}_{1}}}}-\frac{1}{3}{{Z}_{{{C}_{1}}}}\Rightarrow -2{{Z}_{{{L}_{1}}}}=\frac{2}{3}{{Z}_{{{C}_{1}}}} \\ & {{Z}_{{{L}_{1}}}}-{{Z}_{{{C}_{1}}}}=-3{{Z}_{{{L}_{1}}}}+\frac{1}{3}{{Z}_{{{C}_{1}}}}\Rightarrow 4{{Z}_{{{L}_{1}}}}=\frac{4}{3}{{Z}_{{{C}_{1}}}}\Rightarrow {{Z}_{{{C}_{1}}}}=3{{Z}_{{{L}_{1}}}}=3m \\ \end{align} \right.\)
Khi tần số \({{f}_{1}}=25\text{ }Hz\), độ lệch pha giữa cường độ dòng điện và điện áp giữa hai đầu đoạn mạch là:
\(\varphi =\frac{\pi }{2}-\frac{\pi }{3}=\frac{\pi }{6}\Rightarrow \cos \frac{\pi }{6}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( m-3m \right)}^{2}}}}\)
\(\Rightarrow \frac{\sqrt{3}}{2}=\frac{R}{\sqrt{{{R}^{2}}+4{{m}^{2}}}}\Rightarrow 3{{R}^{2}}+12{{m}^{2}}=4{{R}^{2}}\Rightarrow R=2\sqrt{3}m\)
Khi tần số
\({{f}_{3}}=12,5\left( Hz \right)=0,5{{f}_{1}}\Rightarrow \left\{ \begin{align} & {{Z}_{{{L}_{3}}}}=0,5{{Z}_{{{L}_{1}}}}=0,5m \\ & {{Z}_{{{C}_{3}}}}=2{{Z}_{{{C}_{1}}}}=6m \\ \end{align} \right.\)
Công suất tiêu thụ trên mạch là:
\(\left\{ \begin{align} & {{P}_{3}}=\frac{{{U}^{2}}.2\sqrt{3}m}{{{\left( 2\sqrt{3}m \right)}^{2}}+{{\left( 0,5m-6m \right)}^{2}}}=\frac{{{U}^{2}}.2\sqrt{3}m}{42,25{{m}^{2}}} \\ & {{P}_{1}}=\frac{{{U}^{2}}.2\sqrt{3}m}{{{\left( 2\sqrt{3}m \right)}^{2}}+4{{m}^{2}}}=\frac{{{U}^{2}}.2\sqrt{3}m}{16{{m}^{2}}}=50 \\ \end{align} \right.\)
\(\Rightarrow \frac{{{P}_{3}}}{{{P}_{1}}}=\frac{16{{m}^{2}}}{42,25{{m}^{2}}}=\frac{16}{42,25}\Rightarrow {{P}_{3}}=\frac{16}{42,25}{{P}_{1}}=18,93\left( \text{W} \right)\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Hiệp Thành
Copyright © 2021 HOCTAP247
