Một đoạn mạch \(AB\) gồm đoạn \(AM\) và đoạn \(MB\) mắc nối tiếp
Câu hỏi :
Một đoạn mạch \(AB\) gồm đoạn \(AM\) và đoạn \(MB\) mắc nối tiếp, đoạn \(AM\) gồm cuộn dây có điện trở thuần, đoạn \(MB\) chứa điện trở thuần và tụ điện mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \({u_{AB}} = {U_o}{\rm{cos}}\left( {\omega t + \varphi } \right)\) thì đồ thị biểu diễn sự phụ thuộc của điện áp hai đầu đoạn mạch \(AM\) và \(MB\) vào thời gian như hình vẽ. Lúc điện áp tức thời \({u_{AM}} = - 75\sqrt 3 V\) và đang giảm thì tỉ số \(\dfrac{{{u_{AM}}}}{{{U_o}}}\) gần nhất với giá trị nào sau đây?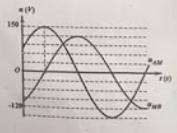
A. \(0,32\)
B. \( - 0,48\)
C. \( - 0,36\)
D. \(0,65\)
* Đáp án
C
* Hướng dẫn giải
Từ đồ thị, ta có: \(\left\{ \begin{array}{l}{U_{0AM}} = 150V\\{U_{0MB}} = 120V\end{array} \right.\)
\({u_{AM}}\) nhanh pha hơn \({u_{MB}}\) một góc \(\dfrac{\pi }{2}\)
\( \Rightarrow \) Điện áp cực đại giữa hai đầu đoạn mạch \({U_0} = \sqrt {U_{0AM}^2 + U_{0MB}^2} = \sqrt {{{150}^2} + {{120}^2}} = 30\sqrt {41} V\)
+ Biểu diễn dao động điện tương ứng trên đường tròn, ta thấy khi \({u_{AM}} = - 75\sqrt 3 V = \dfrac{{ - {U_{0AM}}\sqrt 3 }}{2}\)
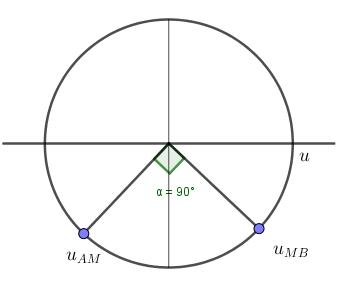
Thì \({u_{MB}} = \dfrac{{{U_{0MB}}}}{2} = \dfrac{{120}}{2} = 60V\)
\( \Rightarrow {u_{AB}} = {u_{AM}} + {u_{MB}} = - 75\sqrt 3 + 60 \approx - 69,9V\)
\( \Rightarrow \dfrac{{{u_{AB}}}}{{{U_0}}} = \dfrac{{ - 69,9}}{{30\sqrt {41} }} = - 0,364\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn tập hè môn Vật Lý 12 năm 2021 Trường THPT Lê Thánh Tông
Copyright © 2021 HOCTAP247
