Bài tập 2 trang 25 SGK Vật lý 12

Bài tập 2 trang 25 SGK Vật lý 12

Phương pháp giản đồ Fre-nen:

• Lần lượt vẽ hai vecto quay biểu diễn hai phương trình dao động thành phần.

• Sau đó vẽ tổng hai vecto trên.

• Vecto tổng là vecto quay biểu diễn phương trình của dao động tổng hợp.

​Cụ thể: 

• Xét 2 dao động cùng phương, cùng tần số:

\(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)

• Dao động tổng hợp \(x =x_1 + x_2 = A \cos (\omega t + \varphi )\)

\(\Rightarrow \overrightarrow{A} = \overrightarrow{A_1} + \overrightarrow{A_2}\ (*)\)

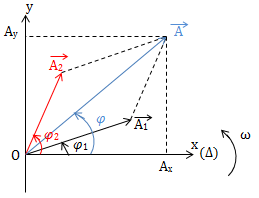
• Chiếu (*) lên: \(\left\{\begin{matrix} Ox: A_x = A_{1x} + A_{2x} \\ Oy: A_y = A_{1y} + A_{2y} \end{matrix}\right.\)

• Với \(A_x = A\cos \varphi ;\ Ay = A\sin \varphi\)

\(\Rightarrow \left\{\begin{matrix} A\cos \varphi = A_1 \cos \varphi _1 + A_2 \cos \varphi _2\\ A\sin \varphi = A_1 \sin \varphi _1 + A_2 \sin \varphi _2 \end{matrix}\right.\)
\(\Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 - \varphi _1)}\)
\(\Rightarrow \tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\)

-- Mod Vật Lý 12