Đề kiểm tra 15 phút - Đề số 14 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7

Đề bài

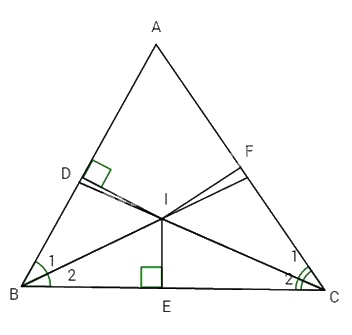
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I.

a) Biết \(\widehat A = {70^o}\). Tính số đo góc \(\widehat {BIC}.\)

b) Vẽ \(ID \bot AB\) (D thuộc AB), \(IE \bot BC\) (E thuộc BC), \(IF \bot AC\) (F thuộc AC). Chứng minh rằng: \(ID = IE = IF.\)

Hướng dẫn giải

a) Ta có \(\widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\)

\( = {180^o} - {70^o} = {110^o}.\)

Do đó \(\dfrac{{\widehat B}}{2} + \dfrac{{\widehat C}}{ 2} = \dfrac{{{{110}^o}} }{ 2} = {55^o}\) hay \(\widehat {{B_2}} + \widehat {{C_2}} = {55^o}.\)

Xét \(\Delta BIC\) ta có \(\widehat {BIC} = {180^o} - \left( {\widehat {{B_2}} + \widehat {{C_2}}} \right) \)\(\,= {180^o} - {55^o} = {125^o}.\)

b) ID, IE lần lượt vuông góc với AB, BC (giả thiết) nên có tam giác BDI, BEI vuông.

Xét hai tam giác vuông BDI và BEI có

+) \(\widehat {{B_1}} = \widehat {{B_2}}\) (giả thiết).

+) BI cạnh chung   

\( \Rightarrow \Delta BDI = \Delta BEI \Rightarrow ID = IE\,\,(1)\)

Chứng minh tương tự ta có cặp tam giác sau đây bằng nhau

\(\Delta CEI = \Delta CFI \Rightarrow IE = IF\,\,(2)\)

Từ (1) và (2) \( \Rightarrow ID = IE = IF.\)