Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 2 - Hình học 7

Đề bài

Bài 1: Cho tam giác ABC vuông tại B có góc \(\widehat {{B_1}} = \widehat {{B_2}}\) \(\widehat A = {60^o}\), kẻ BH vuông góc với AC (H thuộc AC). Qua B kẻ đường thẳng d song song với AC.

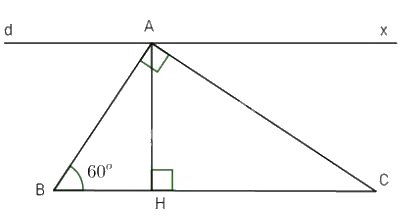
a) Tính góc \(\widehat {ABH}\).

b) Chứng minh d vuông góc với BH.

c) Hãy so sánh góc \(\widehat {ABH}\) và \(\widehat {CBx}\) (theo hình vẽ).

Bài 2:  Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M. Trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh \(\Delta AMN\) là tam giác cân.

b) Kẻ BH vuông góc với AM (H thuộc AM), CK vuông góc với AN (K thuộc AN). Chứng minh rằng BH = CK.

c) Gọi O là giao điểm của BH và CK. Chứng minh  \(\Delta OBC\) cân.

d) Gọi D là trung điểm của BC. Chứng minh rằng A, D, O thẳng hàng.

Hướng dẫn giải

Bài 1:

a) Ta có \(BH \bot AC\) (giả thiết) nên \(\Delta BHA\) vuông tại H có \(\widehat A = {60^o}\) (giả thiết)

\( \Rightarrow \widehat {ABH} = {90^o} - {60^o} = {30^o}\).

b) \(\left\{ \matrix{  d//AC\, (gt) \hfill \cr  BH \bot AC\,(gt) \hfill \cr}  \right. \Rightarrow d \bot BH.\)

c) Ta có \(\widehat {ABH} + \widehat {HBC} = \widehat {ABC} = {90^o}\)(giả thiết)   (1)

lại có \(d \bot BH\) (chứng minh trên) \( \Rightarrow \widehat {CBx} + \widehat {HBC} = {90^o}\) (2)

Từ (1) và (2) \( \Rightarrow \widehat {CBx} = \widehat {ABH} = {30^o}\).

Bài 2: 

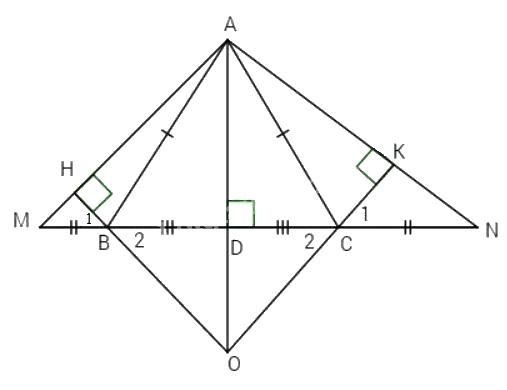
a) Ta có  \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù).

\( \Rightarrow \widehat {ABM} = \widehat {ACN}\).Tương tự \(\widehat {ACN} + \widehat {ACB} = {180^o}\) mà \(\widehat {ABC} = \widehat {ACB}\) (giả thiết).

Xét \(\Delta ABM\) và \(\Delta ACN\) có: AB = AC (giả thiết)

\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên), BM = CN (giả thiết)

Do đó \(\Delta ABM = \Delta ACN\)(c.g.c) \( \Rightarrow AM = AN\) (cạnh tương ứng)

Vậy \(\Delta AMN\) cân tại A.

b) Ta có \(\Delta BHM\) và \(\Delta CKN\) vuông (giả thiết) có \(\widehat {AMN} = \widehat {ANM}\) (chứng minh trên) và BM = CN (giả thiết).

Do đó \(\Delta BHM = \Delta CKN\)(g.c.g) \( \Rightarrow BH = CK\) (cạnh tương ứng).

c) Ta có \(\Delta BHM = \Delta CKN\) (chứng minh trên)

\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\) (góc tương ứng) mà \(\widehat {{B_1}} = \widehat {{B_2}}\)(đối đỉnh).

Tương tự \( \Rightarrow AO\) \(\widehat {{C_1}} = \widehat {{C_2}}\) \( \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\). Chứng tỏ \(\Delta OBC\) cân.

d) D là trung điểm của BC (giả thiết) \( \Rightarrow DB = DC\). Do đó \(\Delta ADB = \Delta ADC\) (c.c.c) \( \Rightarrow \widehat {DAB} = \widehat {DAC}\) hay AD là tia phân giác của góc \(\widehat {BAC}\).

Chứng minh tương tự ta có \(\Delta ABO = \Delta CAO\)(c.c.c) \( \Rightarrow AO\) là phân giác của góc \(\widehat {BAC}\).

Vậy ba điểm A, D, O thẳng hàng.