Bài 64 trang 87 SGK Toán 7 tập 2
Tóm tắt bài
Đề bài
Gọi MH là đường cao của tam giác MNP. Chứng minh rằng: Nếu MN < MP thì HN < HP và \(\widehat {NMH} < \widehat {PMH}\) (yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).
Hướng dẫn giải
- Áp dụng quan hệ giữa các đường xiên và hình chiếu.
- Áp dụng quan hệ giữa cạnh và góc trong tam giác.
Lời giải chi tiết
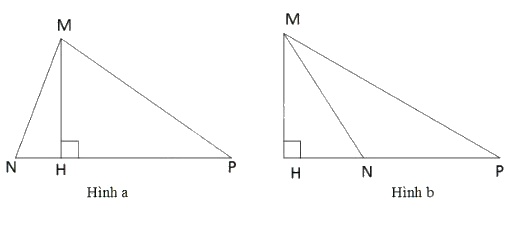
+ Nếu góc N nhọn (hình a)
∆MNP có \(\hat N\) nhọn nên chân đường cao H kẻ từ M nằm giữa N và P.
Ta có hình chiếu của MN và MP lần lượt là HN và HP.
Từ giả thiết MN ∆MNP có MN Lại có \(\widehat {NMH} + \widehat {MNH} = {90^o}\) (∆MNH vuông tại H) (2) \(\widehat {MPH} + \widehat {PMH} = {90^o}\) (∆MHP vuông tại H) (3) Từ (1), (2), (3) suy ra \(\widehat {NMH} + Nếu góc N tù (hình b) ∆MNP có \(\hat N\) tù nên chân đường cao H ở ngoài cạnh NP và N ở giữa H và P \( \Rightarrow\) HN Vì N ở giữa H và P nên tia MN ở giữa hai tia MH và MP. Từ đó suy ra \(\widehat {HMN} (Giải thích ở phần (1; 2; 3): nếu tổng của hai cặp số cùng bằng nhau (bằng \( 90^o\) chẳng hạn) thì số nào cộng với số lớn hơn thì nhỏ hơn số kia. Tức là: \(a + b = 90^o ; \quad \quad c + d = 90^o\) mà \(b > d\) thì suy ra \(a
Copyright © 2021 HOCTAP247
