Bài 69 trang 88 SGK Toán 7 tập 2

Đề bài

Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.

Hướng dẫn giải

Áp dụng tính chất ba đường cao của tam giác.

Lời giải chi tiết

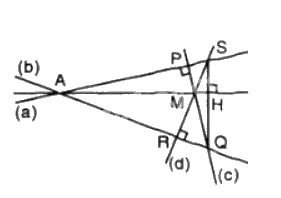
Vì a và b không song song nên giả sử chúng cắt nhau tại A.

Xét ΔAQS có:

    QP ⊥ AS (vì QP ⊥ a)

    SR ⊥ AQ (vì SR ⊥ b)

Ta có QP và RS cắt nhau tại M. Vậy M là trực tâm của ΔAQS.

\( \Rightarrow\) Đường thẳng đi qua M và vuông góc với QS tại H sẽ là đường cao thứ ba của ΔAQS.

Vậy MH phải đi qua đỉnh A của ΔAQS hay đường thẳng vuông góc với QS đi qua giao điểm của a và b (đpcm).