Bài 10 trang 59 SGK Toán 7 tập 2

Đề bài

Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.

Hướng dẫn giải

Áp dụng định lí về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.

Lời giải chi tiết

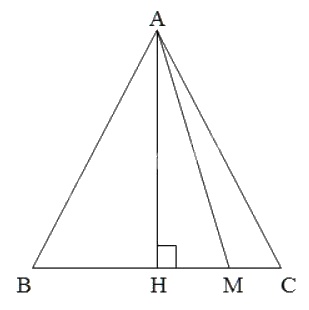
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB; AM ≤ AC.

+ Nếu M  ≡ A hoặc M  ≡  B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M \(\not\equiv\)  B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H \(\Rightarrow \) AM ⊥ BC \(\Rightarrow \) AM

+ Nếu M \(\not\equiv\)  H, giả sử M nằm giữa H và C \(\Rightarrow \) MH

Vì MH và CH là hình chiếu của MA và CA trên đường BC nên MA

Chứng minh tương tự nếu M nằm giữa H và B thì MA

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤  AB, AM ≤  AC.