Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC có ba góc nhọn (\(AB < AC\)). Kẻ AH vuông góc với BC (H thuộc BC). Gọi M là điểm nằm giữa A và H. Tia BM cắt AC ở D. Chứng minh rằng:

a) \(BM < CM\).

b) \(DM < DH\). 

Hướng dẫn giải

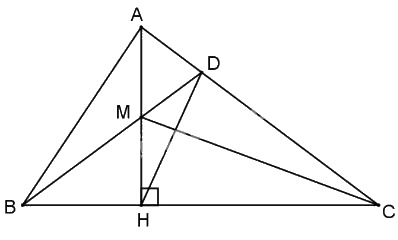
a) \(AB

\(HB

b) Ta có \(\Delta BHM\) vuông tại H nên \(\widehat {BMH}\)  là góc nhọn

\( \Rightarrow \widehat {HM{\rm{D}}}\) là góc tù (vì cùng bù với góc \(\widehat {BMH}\) nhọn).

Do đó trong \(\Delta DMH\) hai góc còn lại phải là góc nhọn hay \(\widehat {MH{\rm{D}}}\) nhọn \( \Rightarrow \widehat {MH{\rm{D}}} \widehat>