Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tia CA lấy điểm E sao cho \(B{\rm{D}} = CE\), nối D với E, kẻ \(DH \bot BC\) (H thuộc BC) CK vuông góc với đường thẳng BC (K thuộc BC). Chứng minh:

a) \(BH = CK.\)

b) \(BC < DE.\) 

Hướng dẫn giải

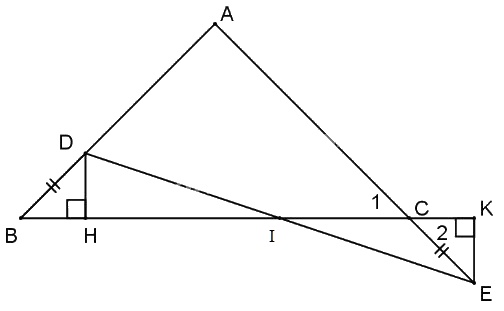
a) Ta có \(\widehat B = {\widehat C_1}\) (gt) và \({\widehat C_1} = {\widehat C_2}\) (đối đỉnh) \( \Rightarrow \widehat B = {\widehat C_2}\).

Do đó hai tam giác vuông \(\Delta BH{\rm{D}} = \Delta CKE\) (ch.gn)

\( \Rightarrow BH = CK\).

b) Ta có \(BC = BH + HC\)

\(HK + HC + CK\), mà \(HB = CK\) (cmt)

\( \Rightarrow BC = HK\).

Ta có \(\Delta DHI\) vuông tại H nên \(HI

Tương tự \(IK

\( \Rightarrow HI + IK

Hay \(HK \),>