Bài 36 trang 87 SGK Toán 8 tập 1

Đề bài

Cho góc xOy có số đo 50⁰, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) So sánh các độ dài OB và OC.

b) Tính số đo góc BOC.

Hướng dẫn giải

- Áp dụng: tính chất hai điểm đối xứng nhau qua 1 đường thẳng, tính chất tam giác cân.

Lời giải chi tiết

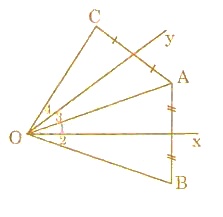
a) Vì B đối xứng với A qua Ox (gt)

\( \Rightarrow \) Ox là đường trung trực của AB \( \Rightarrow \)  OA = OB.

Vì C đối xứng với A qua Oy \( \Rightarrow \) Oy là đường trung trực của AC \( \Rightarrow \) OA = OC.

\( \Rightarrow \) OB = OC.

b)  Vì OA = OB (cmt) \( \Rightarrow \) ∆AOB cân tại O (dấu hiệu nhận biết tam giác cân).

\( \Rightarrow \)\(\widehat{O_{1}}\)= \(\widehat{O_{2}}\)= \(\frac{1}{2}\widehat{AOB}\)

 ∆AOC cân tại O (vì OA = OC)

\( \Rightarrow \) \(\widehat{O_{3}}\)= \(\widehat{O_{4}}\)= \(\frac{1}{2}\widehat{AOC}\)

Do đó \(\widehat{AOB}\) +\(\widehat{AOC}\) = 2(\(\widehat{O_{1}}\)+\(\widehat{O_{3}}\))

                                  = 2\(\widehat{xOy}\)

                                  = 2.50⁰

                                  =100⁰

Vậy \(\widehat{BOC}\) = 100⁰