Giải bài 36 trang 87 - Sách giáo khoa Toán 8 tập 1

Đề bài

Cho góc xOy có số đo 50\(^0\), điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

a) So sánh các độ dài OB và OC

b) Tính số đo góc BOC

Hướng dẫn giải

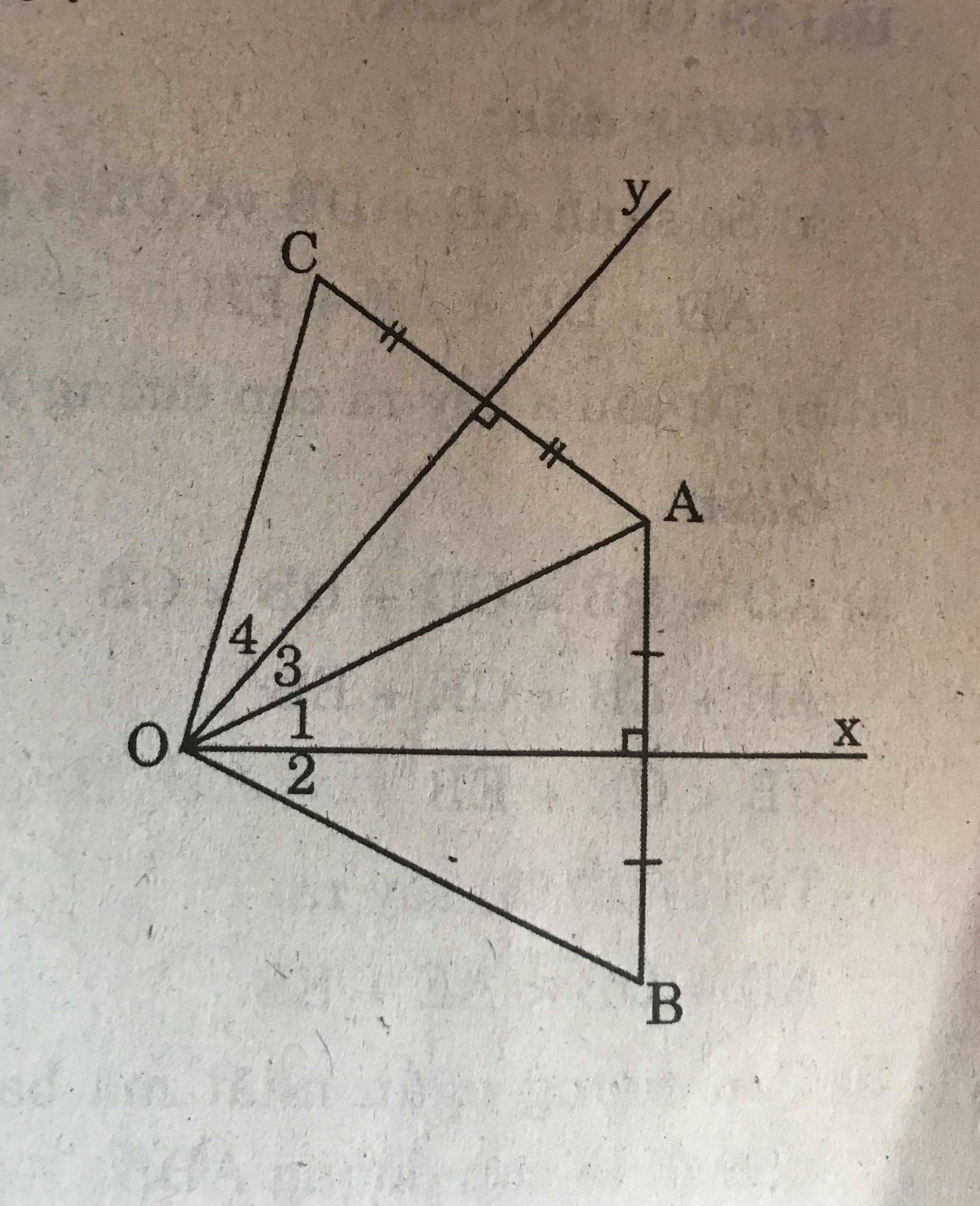
a) B đối xứng với A qua Ox nên Ox là đường trung trực của AB

=> OA = OB 

C đối xứng với A qua Oy nên Oy là đường trung trực của AC.

=> OA = OC

Suy ra : OB = OC

b) \(\triangle\)AOB cân tại O

=> \(\widehat{O_1}=\widehat{O_2}=\dfrac{1}{2}\widehat{AOB}\)

\(\triangle\)AOC cân tại O

=> \(\widehat{O_3}=\widehat{O_4}=\dfrac{1}{2}\widehat{AOC}\)

\(​​\widehat{BOC}=\widehat{AOB}+\widehat{AOC}\)

= 2(\(\widehat{O_1}+\widehat{O_3}\)) = \(2\widehat{xOy}\) = 2.50\(^0\) = 100\(^0\)

Vậy, \(\widehat{BOC}=100^0\)