Bài 84 trang 109 SGK Toán 8 tập 1

Đề bài

 Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gi ? Vì sao ?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?

Hướng dẫn giải

Áp dụng dấu hiệu nhận biết hình bình hành, hình thoi, hình chữ nhật,  hình vuông.

Lời giải chi tiết

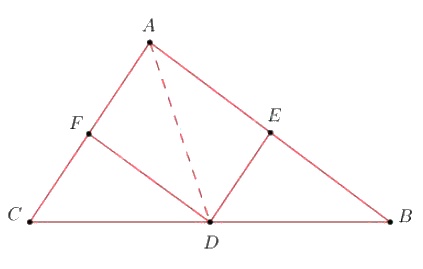
a) Xét tứ giác \(AEDF\) có: 

 \(DE // AF, DF // AE\) (gt)

\( \Rightarrow \)  tứ giác \(AEDF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

b) Hình bình hành \(AEDF\) có \(AD\) là tia phân giác của \(\widehat {CAB}\) hay \(D\) là giao điểm của tia phân giác của  \(\widehat {CAB}\) với \(BC\) thì hình bình hành \(AEDF\) là hình thoi. (dấu hiệu nhận biết hình thoi)

c) Nếu  \(∆ABC\) vuông tại \(A\) thì hình bình hành \(AEDF\) có một góc vuông do đó hình bình hành \(AEDF\) là hình chữ nhật ( theo dấu hiệu nhận biết hình chữ nhật) 

Nếu \(∆ABC\)  vuông tại \(A\) và \(D\) là giao điểm của tia phân giác của góc \(\widehat {CAB}\)  với cạnh \(BC\) thì \(AEDF\) là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).