Bài 35 trang 129 SGK Toán 8 tập 1
Tóm tắt bài
Đề bài
Cho hình thoi ABCD có cạnh AB = 6cm, \(\widehat{A}\) = \(60^{\circ}\)
Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là \(60^{\circ}\)
Hướng dẫn giải
Áp dụng tính chất tam giác đều, định lý pitago, công thức tính diện tích hình thang.
Lời giải chi tiết
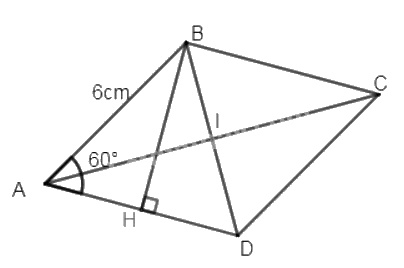
Tính độ dài đường cao BH:
Theo định lí Pitago, tam giác vuông ABH có:
BH2 = AB2 – AH2 = AB2 - \(\left ( \frac{AB}{2} \right )^{2}\)
= AB2 - \(\frac{AB^{2}}{4}\) = \(\frac{3AB^{2}}{4}\).
Nên BH = \(\frac{AB.\sqrt{3}}2{}\) = \(\frac{6\sqrt{3}}2{} = 3\sqrt3\) (cm)
Tổng quát: Đường cao tam giác đều cạnh a có độ dài là: ha = \(\frac{a\sqrt{3}}2{}\)
Tính diện tích hình thoi ABCD.
Cách 1:
Ta có ∆ABC là tam giác đều (tam giác cân có \(\widehat{A}\) = \(60^{\circ}\) ).
Từ B vẽ BH \(\perp\) AD thì HA = HD (tính chất tam giác đều).
Suy ra tam giác vuông AHB là nửa tam giác đều, BH là đường cao tam giác đều cạnh 6cm, BH = \(\frac{6\sqrt{3}}{2} = 3\sqrt 3\) (cm)
Nên SABCD = BH. AD = \(3\sqrt 3. 6 = 18\sqrt 3\) (cm2)
Cách 2:
Vì ∆ABD là tam giác đều nên BD = AB = 6cm, AI là đường cao tam giác nên AI = \(\frac{6\sqrt{3}}{2} = 3\sqrt3\) (cm) \(\Rightarrow AC = 6\sqrt 3\) (cm)
Nên SABCD = \(\frac{1}{2}\) BD. AC = \(\frac{1}{2} 6. 6\sqrt 3 = 18\sqrt 3\) (cm2)
Copyright © 2021 HOCTAP247
