Bài 36 trang 129 SGK Toán 8 tập 1
Tóm tắt bài
Đề bài
Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?
Hướng dẫn giải
Áp dụng: - Công thức tính diện tích hình bình hành, hình vuông.
- Quan hệ đường xiên và hình chiếu trong tam giác vuông.
Lời giải chi tiết
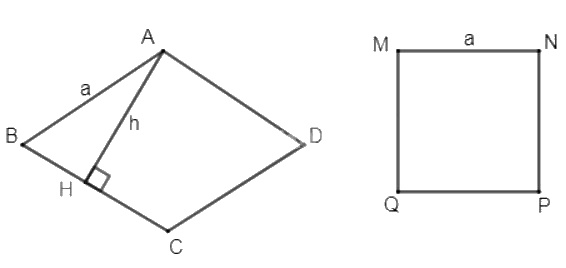
Giả sử hình thoi \(ABCD\) và hình vuông \(MNPQ\) có cùng chu vi là \(4a\).
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là \(a\).
Ta có: \({S_{MNPQ}} = {a^2}\)
Từ đỉnh góc tù \(A\) của hình thoi \(ABCD\) vẽ đường cao \(AH\) có độ dài \(h\).
Khi đó \({S_{ABC{\rm{D}}}} = ah\) (áp dụng công thức tính diện tích hình bình hành)
Nhưng \(h \le a\) (đường vuông góc nhỏ hơn đường xiên) nên \(ah \le {a^2}\)
Vậy \({S_{ABC{\rm{D}}}} \le {S_{MNPQ}}\)
Dấu "=" xảy ra khi \(h = a\) hay \(H\) trùng với \(D\), nghĩa là hình thoi \(ABCD\) trở thành hình vuông.
Copyright © 2021 HOCTAP247
