Bài 3 trang 100 SGK Toán 9 tập 1

Đề bài

Chứng minh các định lý sau:

a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

Hướng dẫn giải

Sử dụng tính chất:

a) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh đó. 

b) Tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó thì là tam giác vuông.

Lời giải chi tiết

a) Xét tam giác \(ABC\) vuông tại \(A\).

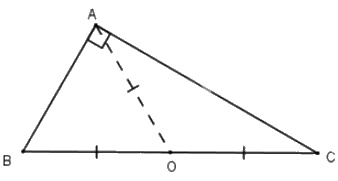
Gọi \(O\) là trung điểm của cạnh huyền \(BC\), ta có:

 \(OB=OC=\dfrac{BC}{2}\).

Lại có, \(\Delta{ABC}\) vuông tại \(A\) có \(AO\) là trung tuyến

\(\Rightarrow AO=\dfrac{BC}{2}\)

Do vậy \(OA=OB=OC=\dfrac{BC}{2}\) nên ba điểm \(A,\ B,\ C\) cùng thuộc đường tròn tâm \(O\) bán kính \(OA\). Hay tâm đường tròn ngoại tiếp tam giác \(ABC\) chính là trung điểm của cạnh huyền.

b) 

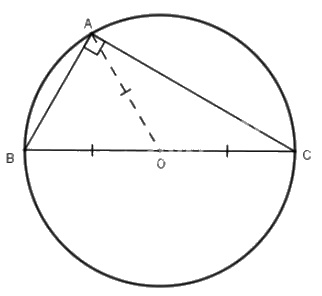
Xét tam giác \(ABC\) nội tiếp đường tròn \((O)\) đường kính \(BC\).

Suy ra ba điểm \(A,\ B,\ C\) cùng nằm trên đường tròn \((O)\)

 \(\Rightarrow OA = OB = OC = R\)

Lại có \(BC\) là đường kính của \((O) \Rightarrow OB=OB=\dfrac{BC}{2}\)

\(\Rightarrow OA=OB=OC=\dfrac{BC}{2}\). 

Vì \(O\) là trung điểm cạnh \(BC\) nên \(AO\) là đường trung tuyến ứng với cạnh \(BC\).

Do đó tam giác \(ABC\) vuông tại \(A\).

Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.