Giải bài 8 trang 101 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
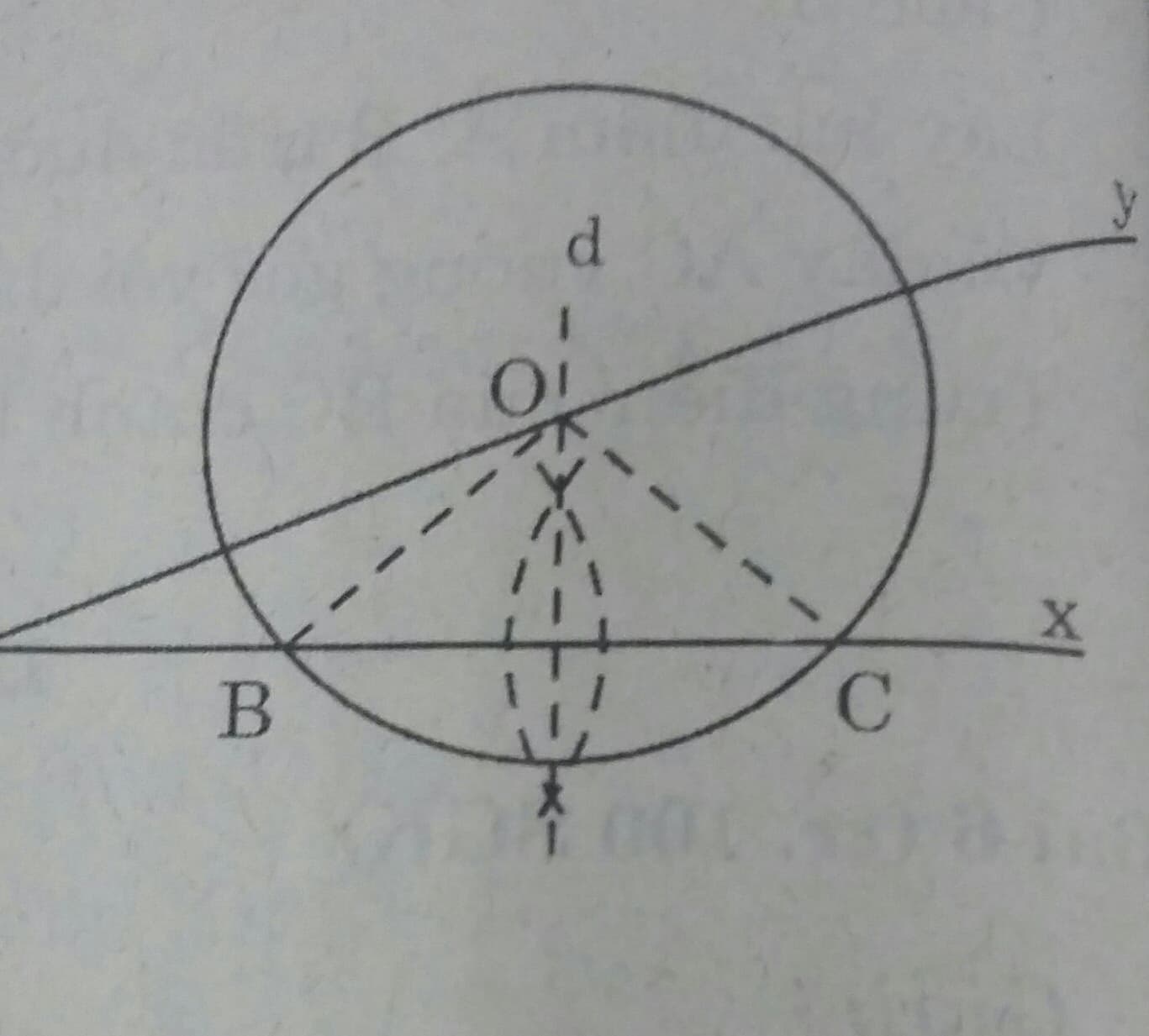
Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Hướng dẫn giải
Hướng dẫn:
Để dựng một đường tròn ta cần xác định tâm và bán kính. Tâm O phải thỏa mãn hai điều kiện, trong đó có một điều kiện nằm trên đường trung trực của BC.
Các bước làm bài toán dựng hình:
Bước 1: Phân tích: Giả sử đã dựng hình H thỏa mãn đề bài. Từ tính chất của hình H suy ra các hình cơ bản cần dựng( các điều kiện mà hình H phải thỏa mãn)
Bước 2: Cách dựng: Nêu cách dựng hình H.
Bước 3: Chứng minh: Hình H có tính chất thỏa mãn đề bài.
Bước 4: Biện luận: Cách dựng hình H có mấy nghiệm hình?
Giải:
* Phân tích:
Giả sử đã dựng được đường tròn (O) thỏa mãn đề bài. Tâm O phải thỏa mãn hai điều kiện:
O nằm trên đường trung trực d của BC. O nằm trên tia Ay.
* Cách dựng:
Dựng đường trung trục d của BC, cắt Ay tại O.
Dựng đương tròn (O; OB) đó là đường phải dựng.
* Chứng minh:
Vì \(O \in d \) nên OB=OC, do đó đường tròn (O;OB) đi qua B và C. Mặt khác: \(O \in Ay \) nên đường trong (O) thỏa mãn đề bài:
* Biện luận:
d cắt Ay tại một điểm O duy nhất nên bài toán có một nghiệm hình.
Copyright © 2021 HOCTAP247
