Giải bài 3 trang 100 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
Chứng minh các định lí sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Hướng dẫn giải
Hướng dẫn:
Áp dụng định lí: Độ dài đoạn trung tuyến kẻ từ đỉnh góc vuông đến trung điểm cạnh huyền trong tam giác vuông bằng nửa độ dài cạnh huyền.
Ta chứng minh ba đỉnh của tam giác vuông cách đều trung điểm của cạnh huyền.
Giải:
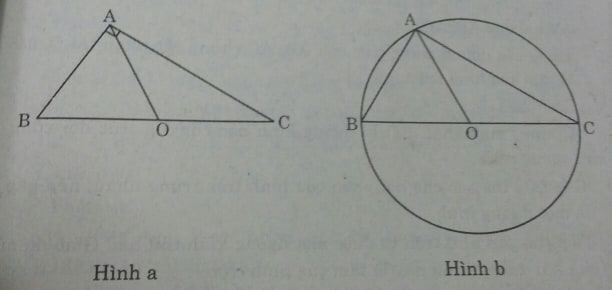
a) (Hình a)
Xét tam giác ABC vuông tại A. Gọi O là trung điểm của cạnh huyền BC.
Ta có: \(OA=OB=OC = \frac{BC}{2}\)
Suy ra: O là tâm của đường tròn đi qua A,B,C. Vậy tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) (Hình b)
Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC.
Ta có OA=OB=OC \( \Rightarrow OA= \frac{1}{2}BC \Rightarrow \Delta ABC \) vuông tại A.
Copyright © 2021 HOCTAP247
