Đề kiểm tra 15 phút - Đề số 4 - Bài 5 - Chương 2 - Hình học 9

Đề bài

Từ điểm A ở ngoài đường tròn (O; R), vẽ tiếp tuyến AB(B là tiếp điểm). Lấy C trên đường tròn sao cho \(AC = AB.\)

a. Chứng minh AC là tiếp tuyến của đường tròn (O)

b. Lấy D thuộc AC. Đường thẳng qua C vuông góc với OD tại I cắt (O) tại E (E khác C). Chứng minh rằng DE là tiếp tuyến của đường tròn (O; R)

Hướng dẫn giải

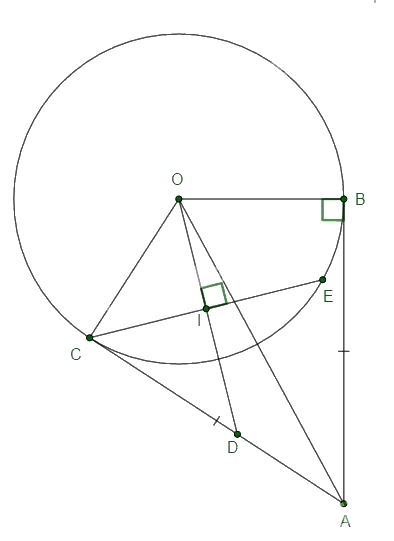
a. Nối O với A. Xét \(∆ACO\) và \(∆ABO\) có:

OA chung

\(OC = OB (=R)\)

\(AC = AB\) (gt)

Vậy \(∆ACO = ∆ABO\) (c.c.c)

\( \Rightarrow \widehat {ACO} = \widehat {ABO} = 90^\circ \)

Chứng tỏ AC là tiếp tuyến của (O)

b. Ta có: \(CE ⊥ DO ⇒ I\) là trung điểm của CE (định lí đường kính dây cung).

Khi đó DO là đường trung trực của đoạn thẳng EC. Do đó \(DC = DE.\)

Theo tính chất của phép đối xứng trục, ta có: \(\widehat {DEO} = \widehat {DCO} = 90^\circ ,\) chứng tỏ DE là tiếp tuyến của (O).