Giải bài 24 trang 111 - Sách giáo khoa Toán 9 tập 1

Đề bài

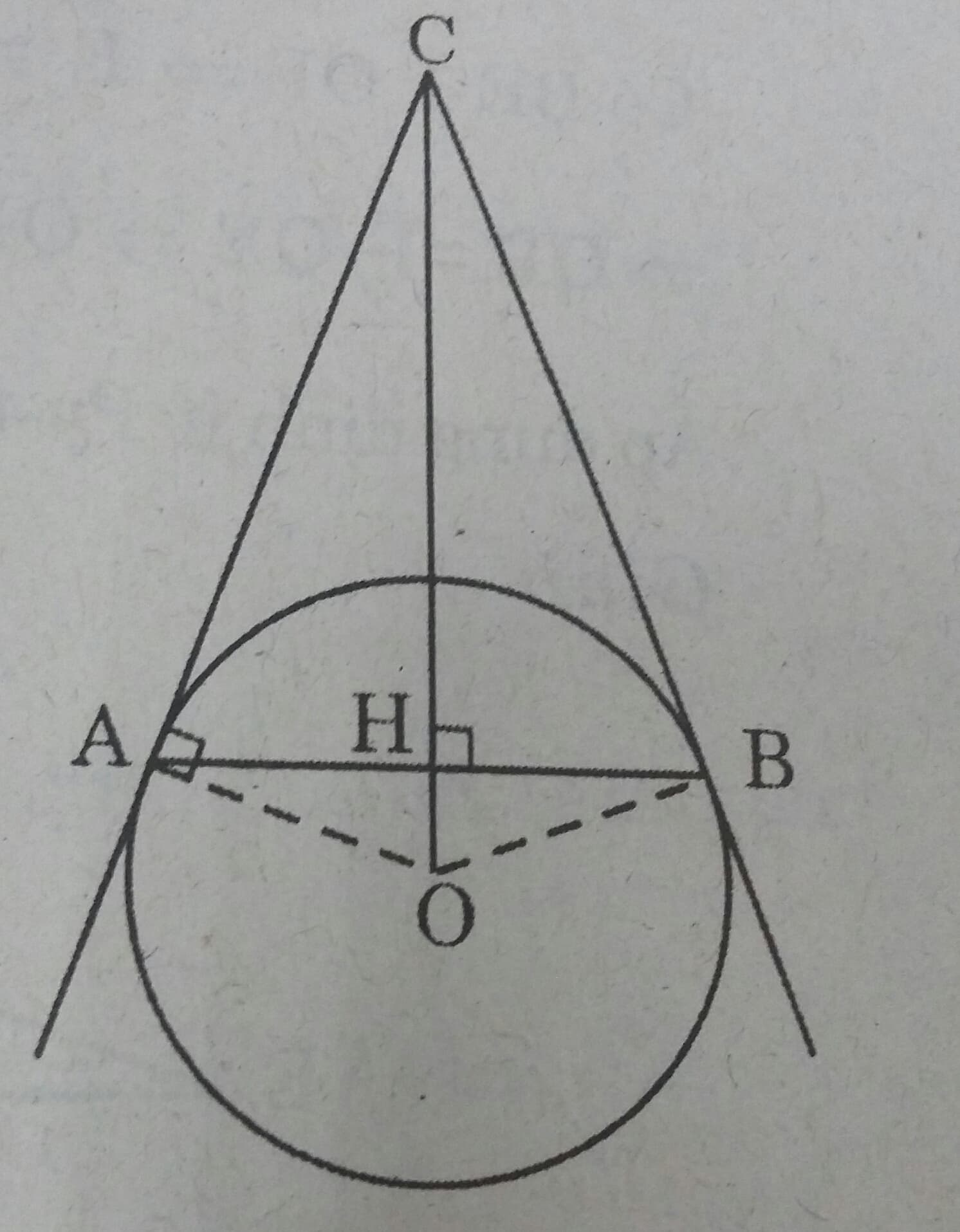
    Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. 

   a) Chứng minh rằng CB là tiếp tuyến của đường tròn.

   b) Cho bán kính của đường tròn bằng 15cm, AB = 24 cm. Tính độ dài OC.

Hướng dẫn giải

   Giải: 

a) \( OC \perp AB \Rightarrow OC\) là đường trung trực AB ( vì đường kính vuông góc với dây cùng thì chia đôi dây cung ấy). 

 Xét \(\Delta OBC \ và\ \Delta OAC\) có OC là cạnh chung HA= HB, CA= CB 

 \(\Rightarrow \Delta OBC = \Delta OAC (c.c.c) \Rightarrow \widehat{OBC}= \widehat{OAC}=90^0\)

 \( \Rightarrow \) CB là tiếp tuyến của đường tròn.

b) \(HA=HB = \frac{AB}{2}= \frac{24}{2}= 12(cm)\)

 Áp dụng định lí Py-ta-go cho tam giác vuông OHA, ta được: 

 \(OH^2=OA^2-HA^2=15^2-12^2 =81 \Rightarrow OH =9(cm)\)

 Áp dụng hệ thức lượng \(c^2= a.c' \) trong tam giác vuông AOC, ta được:   \( OC=\frac{OA^2}{OH}=\frac{15^2}{9}=25(cm) \)