Giải bài 6 trang 69 - Sách giáo khoa Toán 9 tập 2

Đề bài

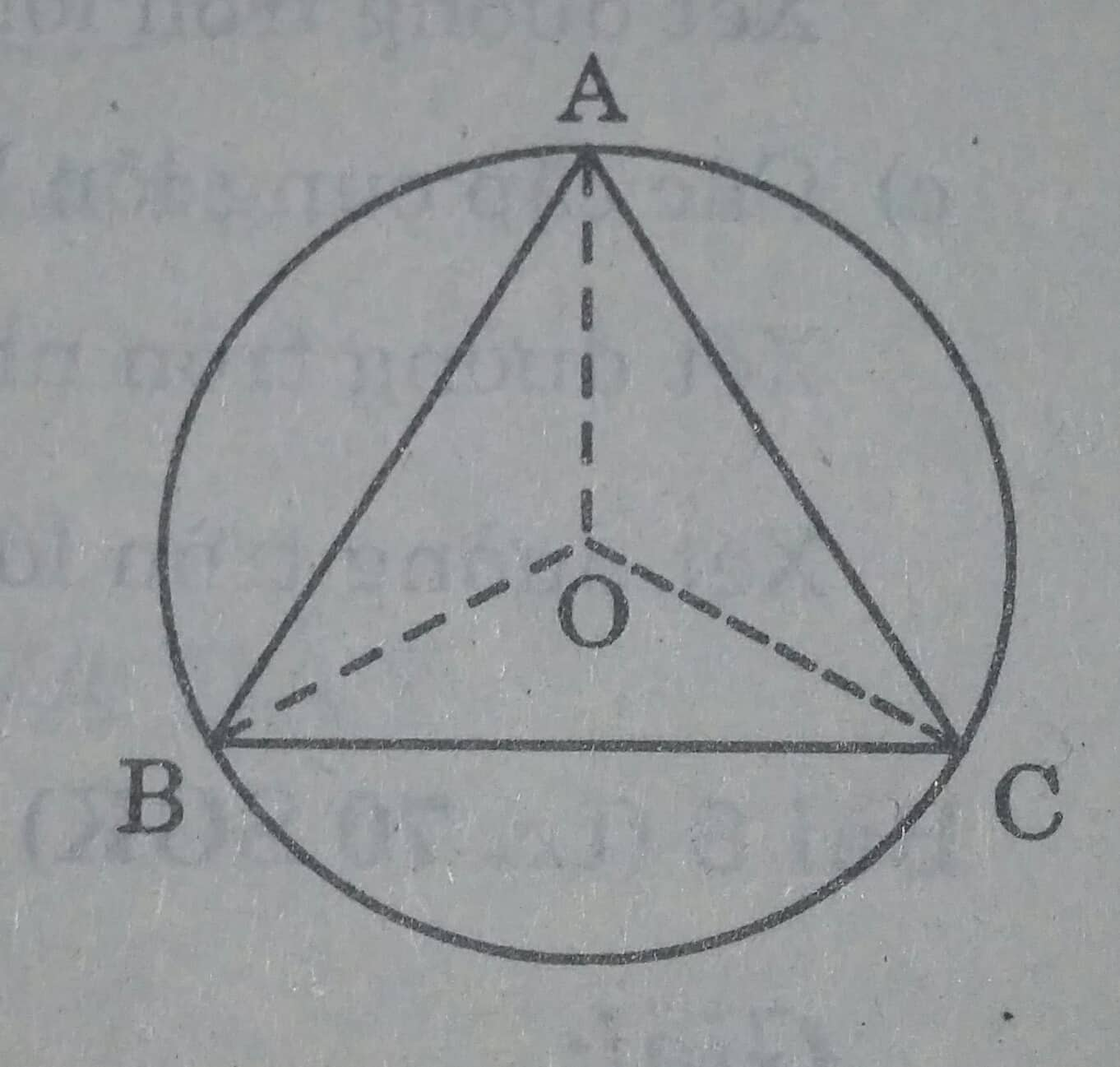
    Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.

   a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.

   b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C

Hướng dẫn giải

     a)  O là tâm của đường tròn đi qua 3 đỉnh A,B,C của tam giác ABC nên OA,OB,OC lần lượt là tia phân giác của các góc \(\widehat{A}, \widehat{B},\widehat{C}. \Rightarrow \widehat{OAB}= \widehat{OBA}= 30^0 \Rightarrow \widehat{AOB}= 120^0 \)( tổng 3 góc trong tam giác bằng \(180^0\))

  Tương tự: \( \widehat{ AOC}=120^0; \widehat{BOC}= 120^0.\)

    b) \( sđ \stackrel\frown{AB}= sđ \stackrel\frown{BC} = sđ \stackrel\frown{AC}= 24^0\)