Bài 39 trang 129 SGK Toán 9 tập 2

Đề bài

Một hình chữ nhật \(ABCD\) có \(AB > AD\), diện tích và chu vi của nó theo thứ tự là \(2a^2\) và \(6a\). Cho hình vẽ quay xung quanh cạnh \(AB\), ta được một hình trụ.

Tính diện tích xung quanh và thể tích của hình trụ này.

Hướng dẫn giải

+) Quay hình chữ nhật quanh một cạnh cố định của nó ta được một hình trụ.

+) Chu vi hình chữ nhật có kích thước \(a, \, b\) là: \(C=2(a+b).\)

+) Diện tích hình chữ nhật có kích thước \(a, \, b\) là: \(S=ab.\)

+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)

+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh +2 \pi r^2.\)

+) Thể tích hình trụ là: \(V=\pi r^2h.\)

Lời giải chi tiết

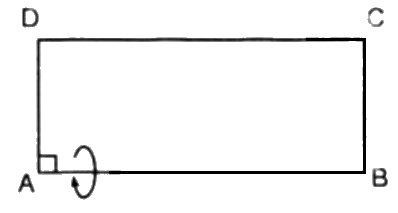
Theo đề bài ta có:

Diện tích hình chữ nhật \(ABCD\) là: \(AB.AD = 2a^2\) (1)

Chu vi hình chữ nhật  là: \(2(AB + CD) = 6a ⇒ AB + CD = 3a\) (2)

Từ (1) và (2), ta có \(AB\) và \(CD\) là nghiệm của phương trình:

\({x^2}-{\rm{ }}3ax{\rm{ }}-{\rm{ }}2{a^2} = {\rm{ }}0\)

Giải phương trình ta được: \({x_1} = {\rm{ }}2a;{\rm{ }}{x_2} = {\rm{ }}a\)

Theo giả thiết \(AB > AD\) nên ta chọn \(AB = 2a; AD = a\)

Khi quay hình chữ nhật quanh \(AB\) ta được hình trụ có \(h=AB=2a\) và \(r=AD=a.\)

Vậy diện tích xung quanh hình trụ là:

\({S_{xq}} = 2\pi .AD.AB = 2\pi .a.2a = 4{\rm{ }}\pi {a^2}\)

Thể tích hình trụ là:

\(V{\rm{ }} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}A{D^2}.{\rm{ }}AB{\rm{ }} = {\rm{ }}\pi .{\rm{ }}{a^2}.{\rm{ }}2a{\rm{ }} = {\rm{ }}2\pi {a^3}\)