Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Ôn tập chương IV – Hình trụ - Hình nón – Hình cầu
Giải bài 39 trang 129 - Sách giáo khoa Toán 9 tập 2
Giải bài 39 trang 129 - Sách giáo khoa Toán 9 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Một hình chữ nhật ABCD có AB > AD, diện tích và chu vi của nó theo thứ tự là 2a2 và 6a. Cho hình vẽ quay xung quanh cạnh AB, ta được một hình trụ.Tính diện tích xung quanh và thể tích của hình trụ này.
Hướng dẫn giải
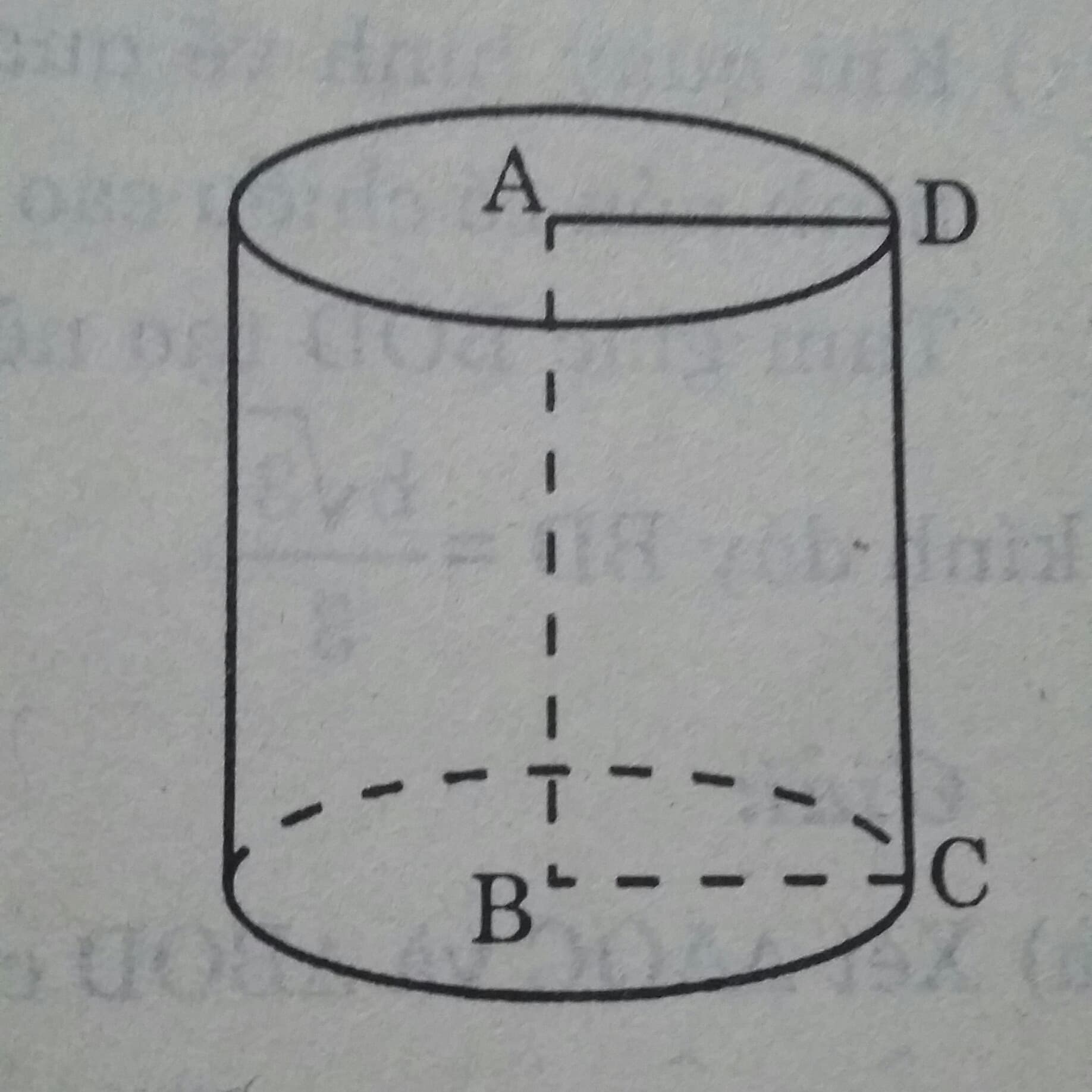
Đặt \(AB = x_1 \ và \ AD = x_2 ( x_1>x_2)\)
Ta có:
\(\left\{\begin{matrix} &x_1 + x_2 = 3a \\ & x_1.x_2= 2a^2\end{matrix}\right.\)
Vậy \(x_1 ; x_2 \) là nghiệm của phương trình bậc hai:
\(x^2 - 3ax+ 2a^2 = 0\)
Giải ta được: \(x_1 = 2a; x_2 = a\)
Khi quay hình vẽ quanh cạnh AB ta được một hình trụ có chiều cao AB = 2a, có bán kính đáy là AD = a.
Vậy:
\(S_{xq}= 2\pi Rh = 2\pi.a.2a= 4\pi a^2;\\ V = \pi R^2 h = \pi .a^2.2a= 2\pi a^3.\)
Copyright © 2021 HOCTAP247
