Chuyên đề về giải bất phương trình và các dạng thường gặp

Chuyên đề về giải bất phương trình và các dạng thường gặp

Bài giảng ngày hôm nay chúng ta cùng nhau tìm hiểu về bất phương trình và cách giải các bài tập liên quan. Mời các bạn cùng đón đọc!

I. Định nghĩa về bất phương trình

    1. Dạng tổng quát

\({\displaystyle f(x)g(x),f(x)\leq g(x),f(x)\geq g(x)}\)

Ví dụ cho BPT \(4.x+ 2 > 0\) nghiệm đúng với mọi số thực \(x> -0.5\). Ta có tập nghiệm:  \({ x{\displaystyle \in \mathbb {R} } | x > -0.5 } = (0.5; {\displaystyle \infty })\).

Công thức liên quan: Bài 6. Phép trừ các phân thức đại số

    2. Phương pháp giải bất phương trình lớp 10

• Bất phương trình bậc nhất một ẩn 

Là bất phương trình dạng: \({\displaystyle a.x+b>0\,}\)

Trường hợp a # 0

- Nếu a > 0, tập nghiệm là: \( {\displaystyle \left({\frac {-b}{a}};+\infty \right)}.\)

- Nếu a < 0, tập nghiệm là: \( {\displaystyle \left(-\infty ;{\frac {-b}{a}}\right)}.\)

Trường hợp a =0

- Nếu b > 0, Phương trình vô số nghiệm.

- Nếu b < 0, Phương trình vô nghiệm.

• Cách giải bất phương trình bậc 2 một ẩn

Là BPT dạng: \({\displaystyle a.x^{2}+b.x+c>0\,}\)với a # 0

Đặt \(Δ = b^2 - 4.a.c\). Ta có các trường hợp sau:

• Nếu Δ < 0:

- a < 0 thì BPT không nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là: \({\displaystyle \varnothing }.\)

- a > 0 thì BPT nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là: \({\displaystyle \mathbb {R} }.\)

• Nếu Δ = 0:

- a < 0 thì BPT không nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là: \({\displaystyle \varnothing }.\)

- a > 0 thì BPT nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là: {\({\displaystyle \mathbb {R} \setminus \left\{{\frac {-b}{2a}}\right\}}.\)

• Nếu Δ > 0, gọi \(x_1, x_2 (x_1 < x_2)\) là hai nghiệm của phương trình bậc hai \(a.x_2 + b.x + c = 0\) với

- \({\displaystyle x_{1}={\frac {-b-{\sqrt {\Delta }}}{2a}};\quad \quad x_{2}={\frac {-b+{\sqrt {\Delta }}}{2a}}}\)

Khi đó: 

- Nếu a > 0 thì tập nghiệm là: \({\displaystyle (-\infty ;x_{1})\cup (x_{2};+\infty )}\)

- Nếu a < 0 thì tập nghiệm là: \({\displaystyle (x_{1};x_{2})\,}\)

II. Bài tập về bất phương trình

Bài 1: Giải bất phương trình chứa căn sau:

\(\sqrt{x(x-1)}+\sqrt{x(x+2)}=2\sqrt {x^2}\)(1)

ĐK: \(x\ge 1\\hoặc \ x\le -2\\hoặc \ x=0\)

(1) \(\Leftrightarrow 2x^2+x+2\sqrt{x^2(x-1)(x+2)}= 4x^2 \Leftrightarrow 2\sqrt{x^2(x-1)(x+2)}=x(2x-1)\\\Leftrightarrow 4x^2(x^2+x-2)=x^2(2x-1)^2\\\Leftrightarrow x^2(8x-9)=0\)

Vậy nghiệm của BPT là x = 0 hoặc \(x=\dfrac{9}{8}\)

Bài 2: Tìm m để bất phương trình có nghiệm duy nhất: \(-\sqrt x-\sqrt{x-1}+2m.\sqrt {x(x-1)}+2\sqrt[4]{x(1-x)}\ge m+m^2\)

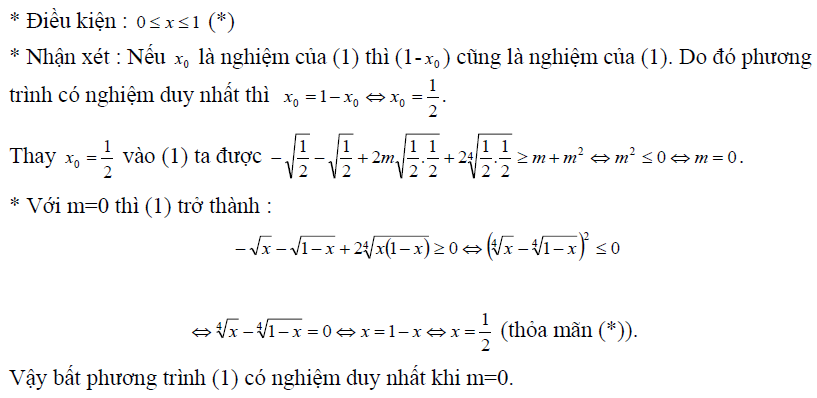
Luyện tập thêm tại: 

• Bất phương trình một ẩn
• Bất phương trình bậc nhất một ẩn

Với những kiến thức tổng hợp trên hy vọng rằng nó đã giúp bạn giải đáp phần nào cách làm dạng bài này như giải bất phương trình chứa dấu giá trị tuyệt đối. Nếu thấy hay nhớ like và chia sẻ nhé. Chúc các bạn có những buổi học vui vẻ!