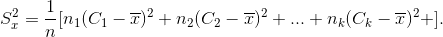Tổng hợp lý thuyết về phương sai đầy đủ và chi tiết
Tóm tắt bài
Trong bộ môn Toán 10, các em sẽ được học về phương sai. Trong bài viết dưới đây, cunghocvui.com sẽ viết về chủ đề này.
1. Phương sai là gì?
Phương sai là số đặc trưng cho độ phân tán của các số liệu so với số trung bình của nó. Phương sai trong bảng thống kê dấu hiệu x có ký hiệu là \(s_x^2\).
2. Công thức tính phương sai
a) Bảng phân bố rời rạc
\(S_x^2 = \dfrac{1}{n}[n_1(x_1 - \overline{x} )^2 + n_2(x_2 - \overline{x})^2 + ... + n_k(x_k - \overline{x})^2] = \dfrac{1}{n}(n_1x_1^2 + n_2x_1^2 + n_2x_2^2 + ... + n_kx_1^2) - (\overline{x})^2\)
+ \(n_i, f_i\) lần lượt là tần số, tần suất của giá trị \(x_i\).
+ n: số liệu thống kê trung bình cộng số liệu đã cho.
+ \(\overline{x}\): số trung bình của bảng.
b) Phân bố tần số ghép lớp
+ \(c_i, n_i, f_i\) lần lượt là giá trị đại diện, tần số, tần suất của lớp thứ i.
+ n là số các số liệu thống kê.
+ \(\overline{x}\): số trung bình của bảng.
3. Bài tập phương sai
Bài 1: Cho hai bảng phân bố tần số ghép lớp:
Khối lượng nhóm cá mè thứ nhất:
Khối lượng nhóm cá mè thứ hai:
Tính số trung bình cộng và phương sai của bảng phân số tần số ghép lớp đã cho.
*Hướng dẫn giải:
Đối với nhóm thứ nhất:
- Số trung bình cộng:
\(\overline{x} = \dfrac{1}{20}.(4.0,7 + 6.0,9 + 6.1,1 + 4.1,3) = 1\)
- Phương sai:
\(S_x^2 = \dfrac{1}{20}(4.0,7^2 + 6.0,9^2 + 6.1,1^2 + 4.1,3^2) -1 = 0,042\)
Đối với nhóm thứ hai:
- Số trung bình cộng:
\(\overline{y} = \dfrac{1}{20}.(3.0,6 + 4.0,8 + 6.1 + 4.1,2 + 3.1,4) = 1\)
- Phương sai:
\(S_x^2 = \dfrac{1}{20}.(3.0,6^2 + 4.0,8^2 + 6.1^2 + 4.1,2^2 + 3.1,4^2) - 1 = 0,064\)
Xem thêm: Giải bài tập phương sai và độ lệch chuẩn
Trên đây là toàn bộ lý thuyết về khái niệm, cách tính phương sai. Rất mong bổ ích đối với độc giả!
Copyright © 2021 HOCTAP247