Bài 10 trang 12 SGK Hình học 10

Đề bài

Cho ba lực \(\overrightarrow {{F_1}}  = \overrightarrow {MA} ,\, \overrightarrow {{F_2}}  = \overrightarrow {MB} \) và \(\overrightarrow {{F_3}}  = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là \(100N\)  và \(\widehat {AMB} = {60^0}.\)

Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} .\)

Hướng dẫn giải

Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:

\(+ )\;\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \) (quy tắc ba điểm).

\( + )\;\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB} \) (quy tắc trừ).

Lời giải chi tiết

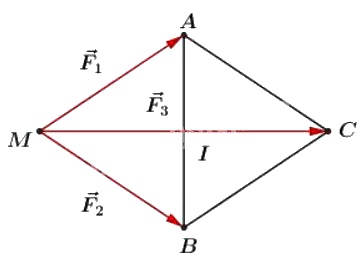
Theo đề bài cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là \(100N\) nên \(MA=MB\). Mặt khác \(\widehat {AMB} = {60^0}\) nên tam giác \(ABM\) đều.

Do đó \( MI={{AM\sqrt 3 } \over 2} = {{100\sqrt 3 } \over 2} = 50\sqrt 3 \)

\(\Rightarrow MC=2MI=2.50\sqrt 3=100\sqrt 3 \)

\(\overrightarrow {{F_3}}  = \overrightarrow {MC}  = \overrightarrow {MA}  + \overrightarrow {MB} \)

Do đó \(\overrightarrow {{F_3}} \) có hướng là tia phân giác trong của góc \(\widehat {AMB} \) và có độ lớn là \(100\sqrt 3 N\)