Bài 6 trang 12 SGK Hình học 10

Đề bài

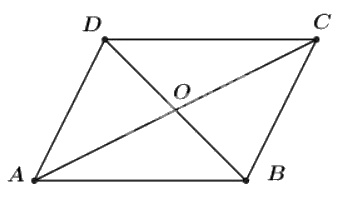
Cho hình bình hành \(ABCD\) có tâm \(O\). Chứng minh rằng:

a) \(\overrightarrow{CO} - \overrightarrow{OB} = \overrightarrow{BA}\);

b) \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{DB}\);

c) \(\overrightarrow{DA}  -\overrightarrow{DB} = \overrightarrow{OD} - \overrightarrow{OC}\);

d) \(\overrightarrow{DA} - \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{0}\).

Hướng dẫn giải

Với quy tắc ba điểm tùy ý \(A, \, \, B, \, \, C\) ta luôn có:

\(+ )\;\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \) (quy tắc ba điểm).

\( + )\;\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {CB} \) (quy tắc trừ).

Lời giải chi tiết

a) Ta có: \(\overrightarrow {CO}  = \overrightarrow {OA}\)\(  \Rightarrow \overrightarrow {CO}  - \overrightarrow {OB}  = \overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {BA} .\)

b) Ta có: \(\overrightarrow {BC}  = \overrightarrow {AD}\)\(  \Rightarrow \overrightarrow {AB}  - \overrightarrow {BC}  = \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB} .\) 

c) Ta có : \(\left\{ \begin{array}{l}
\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {BA} \\
\overrightarrow {OD} - \overrightarrow {OC} = \overrightarrow {CD}
\end{array} \right..\)

Mà \(\overrightarrow {BA}  = \overrightarrow {CD} \)\( \Rightarrow \overrightarrow {DA}  - \overrightarrow {DB}  = \overrightarrow {OD}  - \overrightarrow {OC} .\)

d) Ta có: \(\overrightarrow {DA}  - \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow {BA}  + \overrightarrow {DC}  \)\(= \overrightarrow {BA}  + \overrightarrow {AB}  = \overrightarrow 0 .\)