Bài 6 trang 27 (Hệ trục tọa độ) SGK Hình học 10

Đề bài

Cho hình bình hành \(ABCD\) có \(A(-1; -2), B(3;2), C(4;-1)\). Tìm tọa độ điểm \(D.\)

Hướng dẫn giải

Dựa vào tính chất của hình bình hành và khái niệm hai vecto bằng nhau để làm bài.

Lời giải chi tiết

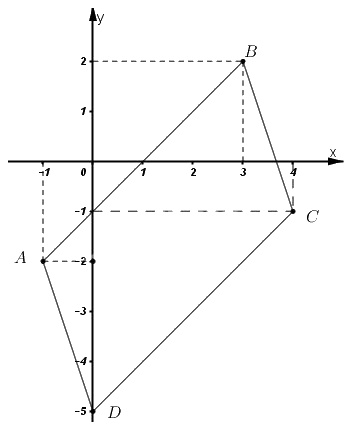
Tứ giác \(ABCD\) là hình bình hành nên 

\(\overrightarrow{CD}=\overrightarrow{BA}\) 

Gọi \((x; y)\) là tọa độ của \(D\) thì

\(\overrightarrow{CD} = (x-4; y+1)\)

\(\overrightarrow{BA}= (-4;-4)\)

\(\overrightarrow{CD}\) = \(\overrightarrow{BA}\)  ⇔ \(\left\{\begin{matrix} x-4 = -4\\ y+1 = -4 \end{matrix}\right.\)  ⇔ \(\left\{\begin{matrix} x=0\\ y=-5 \end{matrix}\right.\)

Vậy điểm \(D(0;-5)\) là điểm cần tìm.