Bài 2 trang 40 SGK Hình học 10

Đề bài

Cho \(AOB\) là tam giác cân tại \(O\) có \(OA = a\) và có các đường cao \(OH\) và \(AK.\) Giả sử \(\widehat {AOH} = \alpha. \) Tính \(AK\) và \(OK\) theo \(a\) và \(α.\)

Hướng dẫn giải

+) Sử dụng công thức lượng giác đối với góc nhọn ta có: \(sin \alpha =\frac{cạnh \, \, đối}{cạnh \, \, huyền}  \) và \(cos \alpha =\frac{cạnh \, \, kề}{cạnh \, \, huyền}\)

Lời giải chi tiết

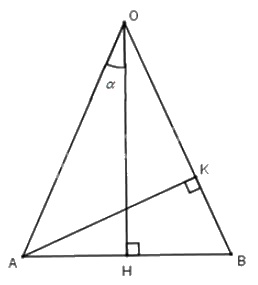
Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\alpha \) 

Tam giác \(OKA\)  vuông tại \(K\) nên ta có:

\(AK = OA.\sin \widehat {AOK} \)\(\Rightarrow AK = a.\sin 2\alpha. \)

\(OK = OA.cos\widehat {AOK} \)\(\Rightarrow OK = a.cos2\alpha .\)